Research
For short videos on cosmology and weak gravitational lensing, see Serious Science.
Much of what we do in science is inference, which means we have some experimental data, from which we infer something about the Universe. For example we may wish to determine how fast the Universe is expanding, or what the properties of Dark Energy are. We can also ask broader questions such as whether the Big Bang model is the preferred theoretical framework, or whether Einstein's General Relativity is favoured over another gravity theory. These are the sorts of questions I and colleagues at the ICIC address, through statistical analysis of cosmological data such as obtained from gravitational lensing, galaxy or microwave background surveys. My specific interests centre on developing and applying the best methods for extracting information from data, such as: using the full

3D information from weak lensing surveys; using the full field values in cosmology, rather than summary statistics, for more accurate and precise inference; compressing data in an optimised way so statistical analysis can be done very fast; looking for non-Gaussianity (NG) in the Cosmic Microwave Background and in the galaxy distribution. We found the NG of the lensing-ISW signal for the first time in the Planck Collaboration (2013; fig. below, with the NG of point sources detected as well). The other scientific questions I am interested in include whether or not the acceleration of the Universe is due to Einstein's cosmological constant, Dark Energy, or alternative gravity models.
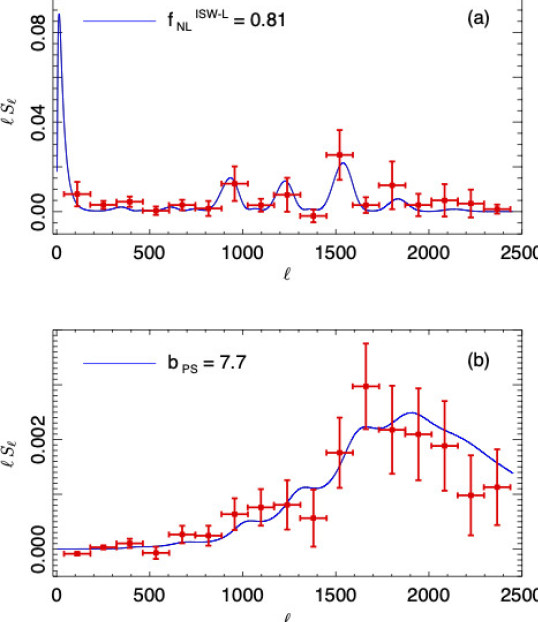
Bayesian Evidence from Planck MCMC chains

In Heavens et al. 2017 we compute Bayesian Evidence (or Marginal Likelihood for cosmological models from the Planck Monte Carlo Markov Chains. The Python code to do this is public here. The full grids of models and datasets analysed are: chains analysed separately, chains concatenated, and a folder of txt and csv files.
If the latest Riess et al (2016) Hubble constant result is added as an additional Gaussian likelihood, then the wCDM model is moderately preferred over standard LCDM, but does not exclude standard LCDM.
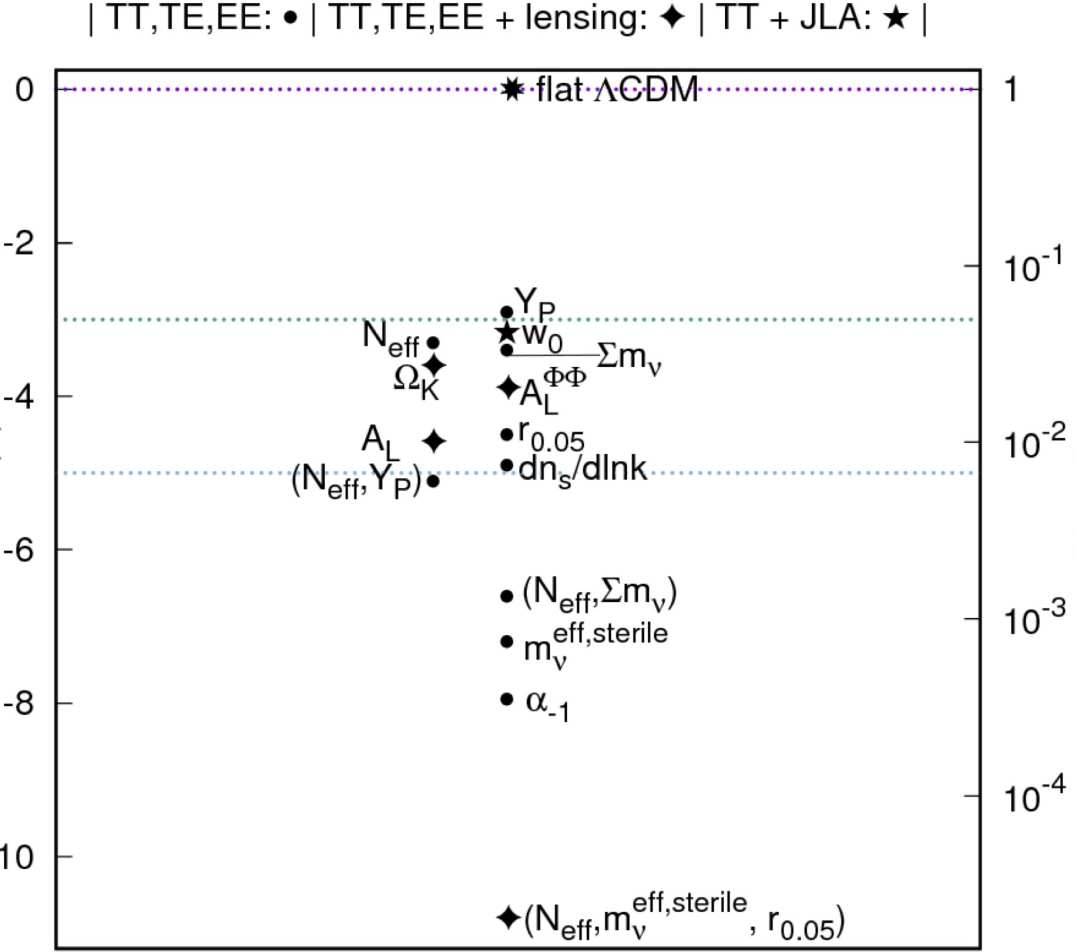
Bayes factors for alternatives to LCDM from Planck MCMC Chains
Baryon Acoustic Oscillation scale


Raul Jimenez, Licia Verde and I have measured the BAO ruler length - a key observable quantity in cosmology theories, in an almost model-independent way from supernova and galaxy clustering data. The length, 101.9 /- 1.9 Mpc/h is measured independently of General Relativity. Published in December 2014 in PRL as Editors' Suggestion, there is an accessible account in their physics highlights. The paper itself is here. Picture courtesy of Chris Blake and Sam Moorfield.
Medical imaging - Blackford

Massive data compression techniques allow very rapid analysis of large data sets, such as come from medical scanners. I am a founding director of Blackford Analysis, a spin-out company from the University of Edinburgh, which specialises in making radiology tasks more efficient.
Bayesian Hierarchical Modelling of weak lensing

The outcome of Bayesian inference is the posterior probability:
PROBABILITY OF WHAT YOU WANT TO KNOW, GIVEN THE DATA AND ANY PRIOR INFORMATION THAT YOU HAVE.
Computing this is usually an interesting challenge, but is now possible for cosmological datasets. In our work, it involves exploring very high-dimensional parameter spaces, of the order of a million dimensions. We do this successfully with Gibbs sampling or Hamiltonian Monte Carlo sampling. Examples are here, in work done with then PhD student Justin Alsing, Andrew Jaffe and colleagues.
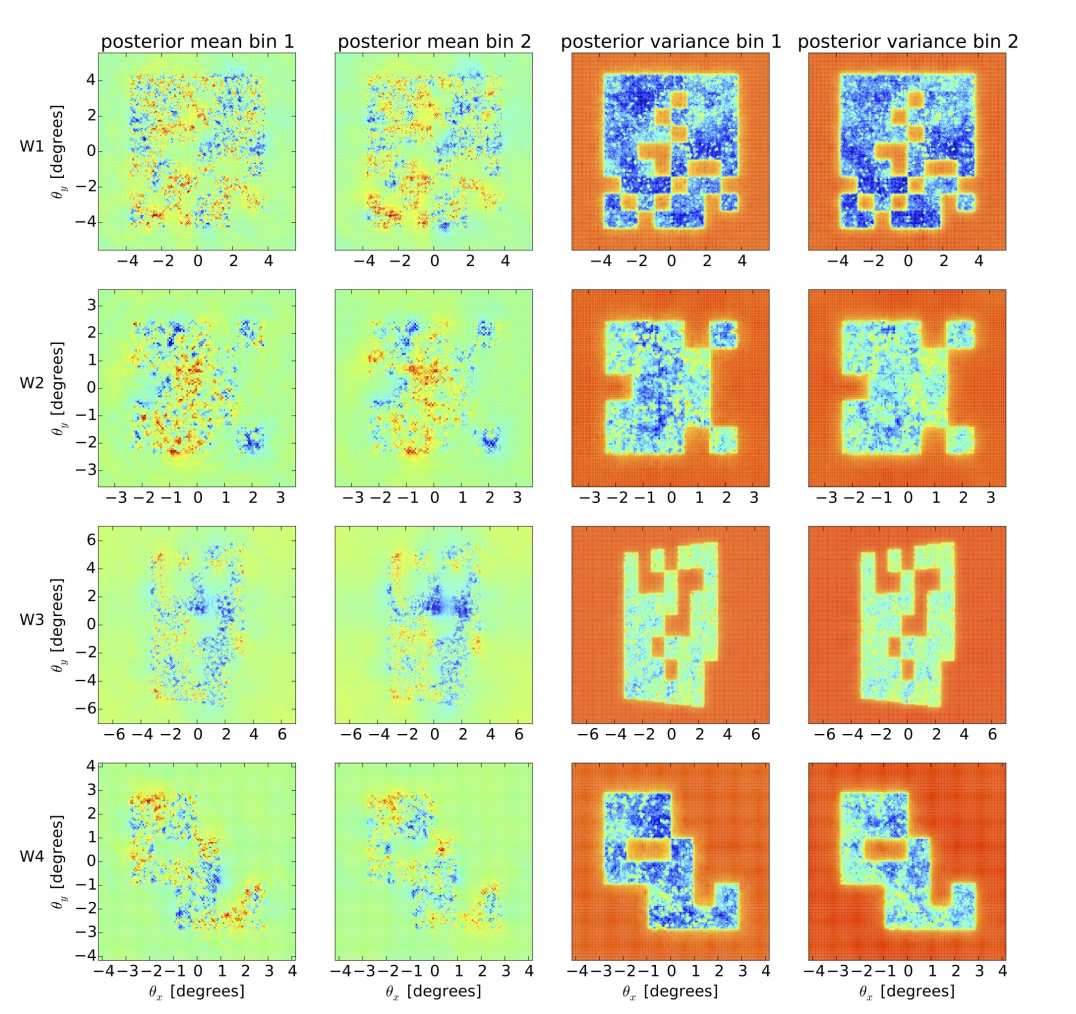
Mass maps and error maps from CFHTLenS weak lensing survey
The Hartlap correction

Gaussian data x are characterised by an expectation value μ and a covariance matrix Σ. Often the covariance matrix is unknown theoretically, and can be estimated in an unbiased way from simulated data. Unfortunately it is the inverse that appears in the gaussian likelihood, and this is biased. The practice in cosmology has been to make this unbiased, by applying the so-called 'Hartlap correction' (Hartlap et al. A&A, 464, 399 (2007); Anderson, An introduction to multivariate statistical analysis (Wiley 2003)), dependent on the number of simulations n, and the number of parameters, p.
This is not the full story, however, and the correct sampling distribution is p(x | μ, Σ'), where Σ' is the estimate of the covariance matrix, which is all that is known. One needs to marginalise over the true (unknown) covariance matrix Σ. This can be done analytically, since Σ' follows a Wishart distribution.
The sampling distribution is not a gaussian at all, but rather a modified t distribution, with wider wings and a narrower core. The details are given in Sellentin & Heavens, MNRAS, 456, 132 (2016).
If you have been using the Hartlap correction, you need to change one line of your code. With the Hartlap correction a=(n-p-2)/(n-1), and χ2=(x-μ)T(Σ')-1(x-μ),
REPLACE
lnL = constant - a χ2/2
WITH
lnL = constant - n ln[1 - χ2/(1-n)]/2
That's all there is to it. For n»p it does not make much difference except in the wings, but one should really get it right.
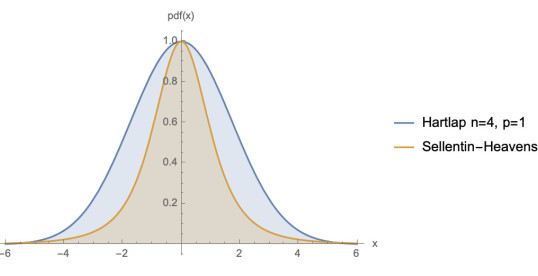
(Not normalised)
This Bayesian analysis is (as always) dependent on the prior choice for the covariance matrix. An alternative to the Jeffreys prior used in Sellentin and Heavens is presented in Percival, Friedrich, Sellentin and Heavens (2022), which gives frequentist-matching posteriors.

