Research
Showcase area
Quantum Reference Frames and Resource Theory of Asymmetry
 It is common in quantum mechanics to assume that clocks and rulers - “reference frames” - with respect to which we measure all systems, are perfect and classical, i.e., large. We have been researching how to treat them in the quantum mechanical formalism and see what type of limitations doing this does or does not impose. In the quantum regime reference frames define consumable resources that may be used for precision controls over small quantum systems, thus giving rise to fundamental limitations above and beyond uncertainty relations. This has interesting foundational consequences in understanding quantum space and time in extreme conditions such as near black holes. However it is also important for building quantum information processing devices! For quantum computers the reference frames often take the form of lasers, and we want to use as small and weak lasers as possible, to miniaturize the devices. Following the research program initiated by Prof. Rudolph and colleagues [Rev. Mod. Phys. 79, 555–609 (2007)] we investigated how long a quantum reference frame (QRF) lasts if it is used as a resource for performing quantum operations and also how we can make it to last longer. We have shown that using the QRF as a reference for measurements causes it to suffer from a back-action which makes the probability of getting the correct measurement result decrease as the number of measurements increases. We have found two different ways of fighting this seemingly inevitable degradation – either through an active corrective mechanism, or by a careful monitoring of the dynamics involved [Phys. Rev. A 82, 032320 (2010)].
It is common in quantum mechanics to assume that clocks and rulers - “reference frames” - with respect to which we measure all systems, are perfect and classical, i.e., large. We have been researching how to treat them in the quantum mechanical formalism and see what type of limitations doing this does or does not impose. In the quantum regime reference frames define consumable resources that may be used for precision controls over small quantum systems, thus giving rise to fundamental limitations above and beyond uncertainty relations. This has interesting foundational consequences in understanding quantum space and time in extreme conditions such as near black holes. However it is also important for building quantum information processing devices! For quantum computers the reference frames often take the form of lasers, and we want to use as small and weak lasers as possible, to miniaturize the devices. Following the research program initiated by Prof. Rudolph and colleagues [Rev. Mod. Phys. 79, 555–609 (2007)] we investigated how long a quantum reference frame (QRF) lasts if it is used as a resource for performing quantum operations and also how we can make it to last longer. We have shown that using the QRF as a reference for measurements causes it to suffer from a back-action which makes the probability of getting the correct measurement result decrease as the number of measurements increases. We have found two different ways of fighting this seemingly inevitable degradation – either through an active corrective mechanism, or by a careful monitoring of the dynamics involved [Phys. Rev. A 82, 032320 (2010)].
In order for a system to be useful as a reference frame it has to be “asymmetric”, in the same way that a rotationally asymmetric object is of use in defining an axis. The utility of physical reference frames in fundamental physics (quantum clocks, phase references, spin dynamics) invariably stems from some underlying, abstract asymmetry. Therefore the study of the QRF inevitably leads to the resource theory of asymmetry – the theory that investigates the advantages of possessing an asymmetric resource state for quantum communication or information processing. Our current work is focused on finding how the asymmetric properties of a system can affect the quantum measurement process, e.g., what is the link between the asymmetry and the uncertainty relations. We have recently shown that using a resource of asymmetry one can overcome the limitation, known as the WAY theorem, enforced on quantum measurements by the conservation laws [New J. Phys. 15 (2013) 013057]. We are also interested in developing the general theory of mixed state asymmetry and linking it with entanglement theory and thermodynamics, as it might be said that while symmetry serves to unify fundamental forces, the asymmetry serves to unify fundamental resources.
Mathematical underpinnings of quantum information theory
 Quantum information has served as a catalyst for many intriguing new developments in mathematics. In some cases, such as random matrix theory, new methods are created to tackle challenging QI problems; in others, such as complexity theory, quantum mechanics provides completely new routes to understanding entirely classical results.
Quantum information has served as a catalyst for many intriguing new developments in mathematics. In some cases, such as random matrix theory, new methods are created to tackle challenging QI problems; in others, such as complexity theory, quantum mechanics provides completely new routes to understanding entirely classical results.
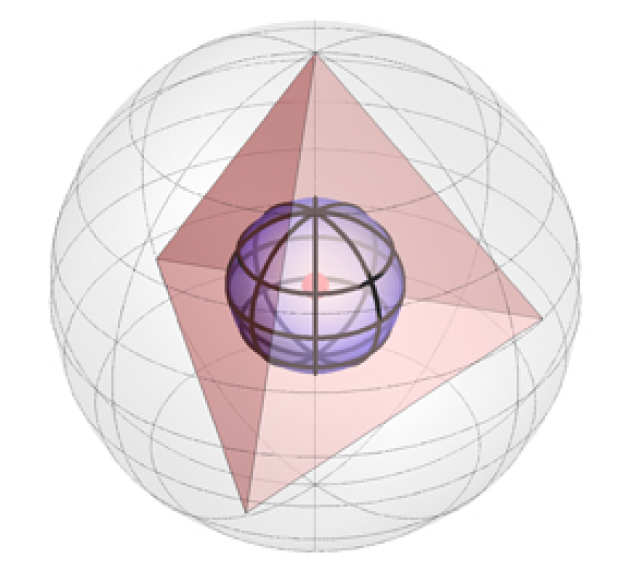
The Werner state on the separable-entangled boundary is represented by a radius 1/3 sphere inside a tetrahedron inside the unit sphere. This reproduces Euler’s 3-dimensional triangle inequality.
By probing the differences between superposition and mixture we gain an illuminated view of what makes quantum mechanics different. The quantum Bernoulli factory uses ideas from exact Monte-Carlo sampling to find situations where quantum processing can accomplish tasks which are impossible classically. The fact that this advantage disappears in approximate sampling problems emphasises the subtle nature of quantum advantage. The more we can learn about situations where the gap between quantum and classical is at its most fragile, the more we will understand what makes quantum mechanics truly spooky.
Robust Computers Made of Light
A quantum paradigm for information pro mises more reliab le communications and enhanced algorithms for many important problems, such as quantum chemistry leading to better drug design, simulation of li ght harvesting comple xes leadin g t o better solar cells or design of new exotic materials capable of withstanding extremes s uch as heat, pressure or electr ical current.
One of our areas of research in the CQD group is trying to bring the quantum computer closer. Our focus is on optical and solid state (semiconductor) systems. Recently [Phys. Rev. Lett.103, 113602 (2009)] we proposed a device at the interface of these two technologies – a “quantum dot machine gun” for entangled photons. This idea captured some media attention and is currently being pursued by three different experimental groups. Even having such a device we still need a robust way of computing with it. To this end we have been investigating how it could be used in a so-called “fault tolerant one-way quantum computer”, a model in which one starts with a three-dimensional lattice of correlated quantum bits and then measures them out following an order dictated by the quantum algorithm, in such a way that the overall shape of the resulting lattice will enact a series of quantum logical gates. We have proposed a way of building of this lattice using arrays of quantum dots – tiny pyramidal structures that are able of firing correlated photons - linear optical gates and very efficient detectors. All these components offer very good controllability and scalability. Simulations have been carried out which suggest that our proposal would be quite robust against errors in the quantum dots, the optical gates and in the detectors.
Quantum Thermodynamics
 Thermodynamics and Information theory are subtly and inextricably linked. Both aim to establish the abstract, and universally valid, patterns and laws that hold irrespective of the particular physical content of a system. The Second Law applies equally well to the whole universe a s it does to delicate quantum systems, and in a similar m anner, information may be encoded equally well in sound waves, supernovae or carved into stone blocks. Rece ntly with cutting-edge developments in Quantum Information theory, ne w ideas and tools are being applied to quantum thermodynamics in a bid to determine the fundamental thermodynamic processes that quantum mechanics allows. Research at Imperial College has analysed how entanglement can distort the thermodynamic arrow in high correlation environments [Phys. Rev. E 81, 061130 (2010)], and how revers ible manipulations of quantum systems may localize useful free energy for efficient use [arXiv:1110.2371v 3], and how non-equilibrium fluctuation theorems apply to quantum systems [arXiv:1204.3571v1]. Current research is focused on problems of what mechanical work actually means in quantum scenarios, how in practice nano-scale quantum systems might function as precision engines or tools, and what abstract structural correspondences exist between the recent resource theory of entanglement and the theory of thermodynamic systems.
Thermodynamics and Information theory are subtly and inextricably linked. Both aim to establish the abstract, and universally valid, patterns and laws that hold irrespective of the particular physical content of a system. The Second Law applies equally well to the whole universe a s it does to delicate quantum systems, and in a similar m anner, information may be encoded equally well in sound waves, supernovae or carved into stone blocks. Rece ntly with cutting-edge developments in Quantum Information theory, ne w ideas and tools are being applied to quantum thermodynamics in a bid to determine the fundamental thermodynamic processes that quantum mechanics allows. Research at Imperial College has analysed how entanglement can distort the thermodynamic arrow in high correlation environments [Phys. Rev. E 81, 061130 (2010)], and how revers ible manipulations of quantum systems may localize useful free energy for efficient use [arXiv:1110.2371v 3], and how non-equilibrium fluctuation theorems apply to quantum systems [arXiv:1204.3571v1]. Current research is focused on problems of what mechanical work actually means in quantum scenarios, how in practice nano-scale quantum systems might function as precision engines or tools, and what abstract structural correspondences exist between the recent resource theory of entanglement and the theory of thermodynamic systems.
Control of interactions in composite quantum systems
The exploitation of quantum mechanics for purposes of quantum information or quantum simulation require precise control of interactions. Fundamentally, the interactions are constant, but we can effectively suppress or enhance interactions, or, even create new types of effective interactions through appropriate manipulation. We are working on the optimal design of time-dependent Hamiltonians for the creation of well-defined interaction mechanisms.
A numerical approach allows us to optimize time-dependencies in an iterative fashion [PRA 88, 052315 (2013)] . With this, we can control the interactions between different species of qubits, create multi-partite entangled states or increase the precision of magnetic field sensing.
If systems are driven with sufficiently high frequency, they behave approximately as if their Hamiltonian was time-independent. In such a regime one can use driving to induce new types of interactions. With suitable techniques to accurately identify effective Hamiltonians [PRL 111, 175301 (2013)] we can find the optimal control strategies to arrive at desirable interactions.
Theory of quantum coherence and multipartite entanglement
Quantum coherence is considered responsible for advanced performance of quantum mechanical systems, ranging from a desired quantum computer up to potentially coherent dynamics of excitations through biomolecular networks. In particular in composite quantum systems, the characterization of quantum coherence requires accurate tools. By now, there is a well-established framework of entanglement measures, that helps us to assess coherence properties of multi-partite quantum states; we are working on the construction of entanglement measures that provide a potentially fine-grained characterization of entanglement properties [PRL 110, 150402 (2013)].
Since destructive interference suppresses transport, whereas constructive interference enhances it, quantum coherence can influence transport properties substantially. The potential of interference to impact transport is limited by the number of coherent path alternatives, i.e. by the coherent delocalization of the propagating object. Similarly to questions regarding multi-partite entanglement, our intuition typically fails us in identifying this number; we therefore work on tools that provide us with a rigorous quantification of coherent delocalization [arXiv 1310.6962].
Quantum coherence and exciton transport
The propagation of an excitation (or any other quantum mechanical (quasi-)particle) through a potential landscape depends sensitively on the exact shape of the landscape and the noise on top. We are interested in geometric features of a landscape that yields well-focussed transport which is potentially robust against external perturbations. Constructive interference of many path alternatives may result in highly directed transport, but the sensitivity against noise increases rapidly with the number of interfering paths.
We have identified geometrical motives that achieve a compromise of good transport properties and robustness [Nat. Comm. 4, 2296 (2013)]. In particular, molecular networks are strongly exposed to noise, so that an enhancement of transport based on coherence and interference is being doubted. With our recently developed tools to characterize quantum coherence, we could verify a supporting role of quantum coherence even in the presence of incoherent driving and strong dephasing [N.J.Phys. 15, 093202 (2013)].
Non-Gaussian Continuous-Variable Quantum Information & Quantum State Engine
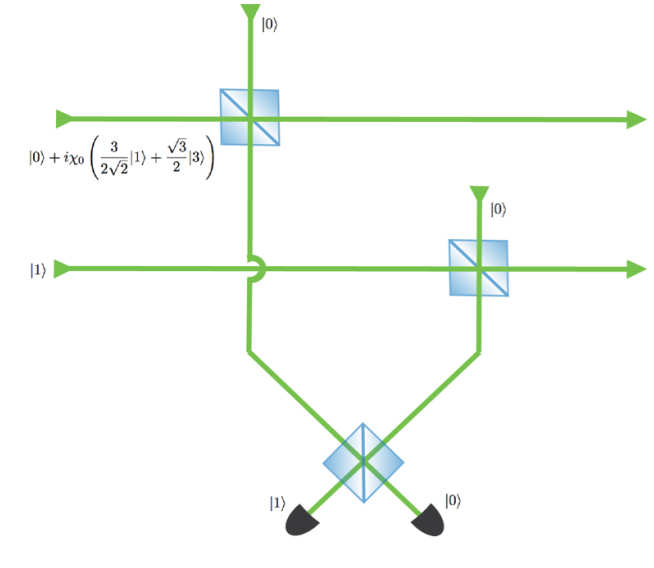
In the field of continuous variable quantum optics, most theoretical investigations revolve around the use of Gaussian states and the Gaussianity-preserving operations of beamsplitting, squeezing and linear amplification. While Gaussian states and operations are particularly nice to work with, for scenarios involving universal quantum computation and communication using entanglement distillation and swapping, quantum memory and teleportation, more sophisticated tools are required. Furthermore, it was demonstrated that any circuit with Gaussian inputs and operations can be efficiently simulated on a classical computer. For universal quantum computing in the continuous variable regime it is therefore necessary to have some non-Gaussianity. This can appear in the form of photon-counting measurements either to generate non-linearities or to prepare offline non-Gaussian ancilla states. These are methods of quantum state engineering.
Current research in the group is looking at implementing non-linear phase gates using offline resource state preparation. In particular, the resource state being considered has a cubic Hamiltonian, as access to this non-linearity is sufficient to realise arbitrary unitary operations of the quantum harmonic oscillator. We look into mixing this order Hamiltonian across multiple modes, seeking a general approach to production of non-linearities in a quantum optics circuit. These approaches are determined based on experimental feasibility.
Open Quantum Systems
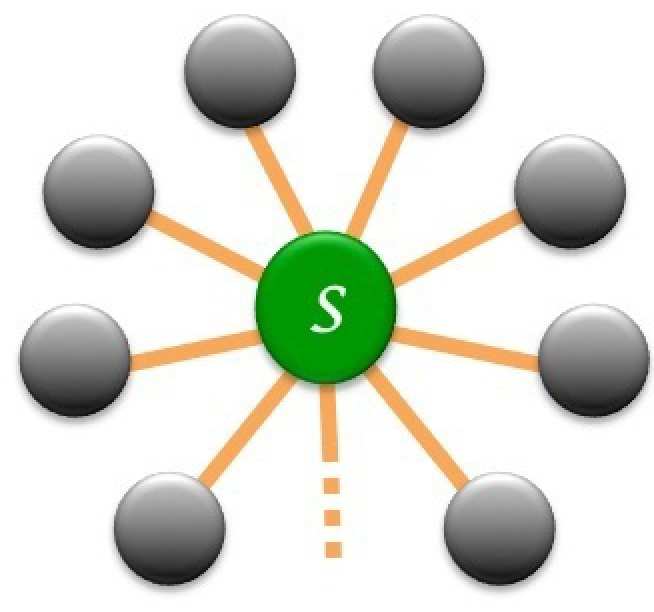
A quantum mechanical system is called open when it interacts with an environment (a large external quantum system). Mos t realistic systems are open quantum systems (OQS) as it is very difficult for th em to be completely isolated from surrounding effects. This interaction with the environment will affect the system in a non-negligible way. Usually the result is the un-recoverable loss of the system’s quantum information but in some cases information can return to the system. Understanding these processes is vital when attempting to build quantum devices and therefore the study of OQS is a very pertinent topic.
In this field our work was based on non-Markovian behaviour (NMB), which considers how memory affects system dynamics. By considering models consisting of coupled harmonic oscillators, the aim was to gain a better understanding of NMB and find possible ways to control it [J. Phys. B: At. Mol. Opt. Phys. 47 015501].
Currently we are also working on the role of counter rotating terms and ultra strong coupling in affecting system dynamics of OQS.
Multi-dimensional Quantum Walk for Quantum Information Processing
We are interested in the use of multi-dimensional quantum walks for the processing of quantum information, in particular in a scenario with only limited resources. Among the deliverables of our research, an important place is taken by the design of testable experimental setups in systems of linear optics. Theoretically, our investigation will provide the tools for the understanding of the resources needed in the simulation of a complex yet interesting quantum dynamical process. The classical random walk is a fundamental process in statistical mechanics, finding applications in various fields, from physics to computer science, from economics to biology. Its quantum mechanical version, or quantum walk, is based on the use of a quantum mechanical system embodying the walker and the coin. Quantum walks have recently raised considerable attention in the widest physical community due to their potential use in the design of new quantum algorithms. Moreover, multi-dimensional quantum walks have been proposed in order to efficiently generate entanglement, a critical requirement for quantum metrology and quantum information processing. Yet, the experimental realisation of known multi-dimensional quantum walks is extremely challenging, due to the significant technological effort required. Tackling the problem of reducing the resources needed for their implementation will provide an experimental-friendly scenario that could significantly contribute to the advancement of quantum information science (see, for instance,[Phys. Rev. Lett. 106, 080502] and its experimental realisation [Nat. Comm. 4, 2471]).
Quantised Light-Matter Interaction
Cavity QED and Waveguide QED are remarkable test-beds to investigate light-matter interactions at the quantum level. On the one hand, the confinement of the EM to one or zero dimensions drastically simplifies the theoretical treatment, which allows for a detailed understanding of processes involving the interaction between a small number of atoms and photons. On the other hand, it is in these simplified geometries that some of the most prominent quantum effects take place, such as the collapses and revivals of atomic excitations, the observation of “Schrodinger cat states” or the possibility of an atom to perfectly reflect a single photon. In our group, we study a variety of dynamical processes involving QED interactions in confined geometries. Our aim is to improve our theoretical understanding of light-matter interactions, as well as our ability to exploit them in Quantum technologies.


