Sum-Of-Squares Approach to Global Stability and Control of Fluid Flows
Student Corner
This page is created and supported by Lyudmila Chernyshenko, a first-year undergraduate student of the Mathematics and Mechanics Faculty of the Saint Petersburg State University. The materials on this page are aimed at undergraduate students.
We begin with the idea:
The Sum of Squares Decomposition
In this section we give a brief introduction to sum of squares polynomials technique introduced in Pablo Parrilo’s thesis in 2000 [1], and show how the existence of a sum of squares decomposition can be verified using semidefinite programming.
Note: Semidefinite programming is a subfield of convex optimization concerned with the optimization of a linear objective function (that is, a function to be maximized or minimized) over the intersection of the cone of positive semidefinite matrices with an affine space.
Definition: for х ϵ Rn a multivariate polynomial p(x)is a sum of squares if there exist polynomials fi(x) i=1, … ,M such that
p(x)=![]()
Proposition: A polynomial p(x) of degree 2d is a sum of squares if and only if there exists a positive semidefinite matrix Q and a vector of monomials Z(x), containing monomials of the form ax1r1x2r2...xnrn, where r1+...rn ≤ d such that p(x)=ZT(x)QZ(x).
In general, the monomials in Z(x) are not algebraically independent. Expanding ZT(x)QZ(x) and equating the coefficients of the resulting monomials to the ones in p(x), we obtain a set of affine relations in the elements of Q. The problem of finding a semi-definite matrix Q, the elements of which satisfy the obtained affine relations, can be solved using semi-definite programming. As soon as we find that for p(x) there exists a corresponding positive-semidefinite matrix Q, it is proved that p(x) can be represented as a sum of squares.
Info:
- 1. A self-adjoint matrix is a square complex-valued matrix that is equal to its own conjugate transpose: AT=A. That is, aij=aji for any i and j.
- A n×n self-adjoint matrix A is said to be positive semi-definite if xTAx ≥0 for all х ϵ Rn.
- The number λ is called the eigenvalue or a characteristic value of А, and a vector x≠0 is called an eigenvector or a characteristic vector of А, if Ах=λx.
-
A self-adjoint matrix has only real eigenvalues, and there exists an orthonormal basis e1,…,en such that e1,…,en are the eignevectors of this matrix.
In this basis the matrix is diagonal:
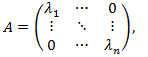 that is aij=0 if i≠j, and λ1, … , λn are the eigenvalues of A.
that is aij=0 if i≠j, and λ1, … , λn are the eigenvalues of A. - A diagonal matrix А is positive-semidefinite if and only if its eigenvalues are non-negative. For proving this it suffices to consider the expression xTAx for any x ϵ Rn:
хTАх=
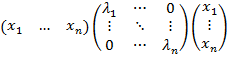 =
= 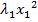 +…+
+…+ 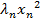 , and
, and 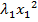 +…+
+…+ 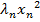 ≥0 is valid for all xif and only if
≥0 is valid for all xif and only if 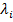 ≥0.
≥0. - A self-adjoint matrix is positive semidefinite if and only if its eigenvalues are nonnegative (directly follows from the statements 5 и 6).
Example (from [2]): Suppose that we want to know whether or not the quartic polynomial in two variables p(![]() ) =
2
) =
2![]() +2
+2![]() -
-![]() +5
+5![]() is a sum of squares.
For this purpose, define
Z(x)=
is a sum of squares.
For this purpose, define
Z(x)=![]() Т
and consider the following quadratic form:
Т
and consider the following quadratic form:
p(![]() ) =
2
) =
2![]() +2
+2![]() -
-![]() +5
+5![]() = Z(x)Т
= Z(x)Т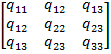 Z(x)
=
Z(x)
= ![]() +
+ ![]() +
+ ![]() +2
+2 ![]() +2
+2 ![]() .
.
From this we get the following relations:
![]()
![]()
![]()
![]()
![]() Now, using semi-definite programming, we can find
Now, using semi-definite programming, we can find
![]() and
and ![]() ,
satisfying the last equation and such that the matrix Q is positive semi-definite. These conditions are satisfied with
,
satisfying the last equation and such that the matrix Q is positive semi-definite. These conditions are satisfied with ![]() и
и ![]() .
After that we find a basis in which matrix Qwill be diagonal. Monomials in Z(x) can be expressed as a linear combination of the basis vectors. By the formula p(x)=Z(x)TQZ(x) we obtain the following sum of squares decomposition:
.
After that we find a basis in which matrix Qwill be diagonal. Monomials in Z(x) can be expressed as a linear combination of the basis vectors. By the formula p(x)=Z(x)TQZ(x) we obtain the following sum of squares decomposition:
p(![]() ) =
) = ![]() .
.
Note: p(x) being sum of squares implies that p(x)≥0 for all х ϵ Rn. However, the converse is not always true. Not all nonnegative polynomials can be written as sum of squares, apart from three special cases:
- n=2, i.e. in two-dimensional space.
- deg(p)=2, i.e. the degree of the polynomial p(x) is two.
- n=3 and deg(p)=4, i.e. the space is three-dimensional and the degree of the polynomial p(x) is four.
As we have already mentioned, a semidefinite matrix, such that its elements satisfy a given set of affine relations, if exists, can be found using semidefinite programming. This is so because the set of positive-semidefinite matrices is convex.
Info: A set is convex if for every pair of points within the set, every point on the straight line segment that joins the pair of points is also within the set. In other words, a set G ϵ Rn is convex if for every pair of points x1 ϵ G, x2 ϵ G and for any λ, 0≤λ≤1 it is true that λx1+(1-λ)x2 ϵ G. |
For verifying this we take two matrices from this set, ![]() and verify that the matrix A=
and verify that the matrix A=![]() +
+![]() , where 0≤λ≤1, will also be positive semidefinite.
Consider xТAx= xТ
, where 0≤λ≤1, will also be positive semidefinite.
Consider xТAx= xТ ![]() +
+![]() )x, where 0≤λ≤1. Since the matrices
)x, where 0≤λ≤1. Since the matrices ![]() are positive-semidefinite and because of the conditions on λ, we obtain that xТAx≥0, which means that the matrix A is positive semidefinite. Hence, the set of such matrices is indeed convex.
are positive-semidefinite and because of the conditions on λ, we obtain that xТAx≥0, which means that the matrix A is positive semidefinite. Hence, the set of such matrices is indeed convex.
We are looking for a matrix from convex set of positive-semidefinite matrices such that the elements of this matrix satisfy a set of affine relations. Since affine relations form a hyperplane, the desired matrix is located in the intersection of a convex set of positive semidefinite matrces and a hyperplane. This intersection will be convex, so the problem of searching for the matrix can indeed be solved using semidefenite programming.
This page is based on [2].
1. P. A. Parrilo. Structured Semidefinite Programs and Semialgebraic Geometry Methods in Robustness and Optimization. PhD thesis, California Institute of Technology, Pasadena, CA, 2000.
2. A. Papachristodoulou and S. Prajna. A Tutorial on Sum of Squares Techniques for Systems Analysis. 2005 American Control Conference June 8-10, 2005. Portland, OR, USA.
Latest:
- The project has ended.
- Paolo Luchini visited us on February 2016.
- Mihailo Jovanovic and Armin Zade visited us during the two weeks 2-15 November 2015.
- All our postdocs secured positions which will allow them to contninue working in cooperation with us: Deqing Huang will be a full professor at the Southwest Jiaotong University, China, Davide Lasagna will be a Frontier Fellow at the Universiy of Southampton, UK, and Giorgio Valmorbida will move to a faculty position at the Supelec and Paris-Sud University, France. Well done!
- Next progress meeting on February 23.2015.
- Remote conference was held on 5.02.2015.
- Sergei was at UCLA attending the Mathematics of Turbulence programme. He gave two presentations about the project.
- Remote conference was held on 30.10.2014.
- Remote conference was held on 09.06.2014.
- A progress meeting was held at Imperial College on 27.03.2014.
- Charles Doering is at Imperial 25-27.03.2014 and in Oxford 27-28.03.2014 He is giving a talk on 26.03, see "Miscellaneous".
- Remote conference was held on 14.03.2014.
- Sergei gave a talk at the NeZaTeGiUs conference NeZaTeGiUs conference on 02.03.2014.
- Deqing went to China 26-30 December and gave a talk at a workshop organized by the State Key Laboratory of Industrial Control Technology, Zhejiang University, Hangzhou.
- Remote conference was held on 20.12.2014 The record is available from Sergei.
- Paul visited London and Oxford for two weeks in October, and took part in the project meeting on 21.10.
- Sergei gave a talk at ICNAAM 2013.
- Remote conference was held on 19.09.2013 The record is available from Sergei.
- Remore conferences were video recorded on 14.05, 06.06, 25.06, 11.07, 16.08, and 21.08.2013 The records are available for the members of the team from Sergei, but the records are not in the repository, to save space.
- July 2013. Deqing gave a talk at the School of Aeronautics and Astronautics, Zhejiang University, Hangzhou, China.
- June 5 and 6, 2013. Our remote conference was spread over 2 days this time.
- May 19-31, 2013. Sergei was in Stockholm, taking part in NORDITA Stability and Transition programme, and the follow-on SIG-33 workshop, where he gave a talk on using SoS in fluid dynamics.
- May 14, 2013. We had our first remote conference. It was interesting, and useful. Giorgio, Davide, and Deqing presented, and we all had a good chat.
- April 22, 2013. SVN repository for the project was created by Paul, hosted at ETH.
- Kick-off meeting on April 18 went fine.
- Paul is here!
- Paul Goulart will be visiting Imperial from April 15 to May 3.
- 30.03.2013 This website opens.
- 28.03.2013 Project mailing list created.
- 11-15.03.2013 Wynn visited Doering in Michigan. <
- 19.02.2013 Chernyshenko visited Southampton team.