FETCH2
FETCH2 is the latest coupled fluids/radiation transport finite element code being developed by the AMCG, building upon the lessons learnt in the original FETCH (Finite Element Transient Criticality, which is outlined below). Some of the novel features of the FETCH2 framework include:
- Solves first order form of the Boltzmann Transport Equation
- Coupled to single-phase CFD through Fluidity
- Use of a low-memory sub-grid scale finite element method for spatial discretisations in general applications
- Adaptivity in space and angle, that can adapt independently across energy
- Several angular discretisations, including Pn, filtered Pn, finite-element and wavelet discretisations
- The Pn and filtered Pn can adapt their order across space/energy, providing more accuracy where needed
- The filtered Pn discretisation combined with angular adaptivity uses spatially-dependent filter strengths without a priori knowledge to keep high-order convergence where smooth, providing fast ray-effect free solutions even in problems with strong discontinuities/streaming.
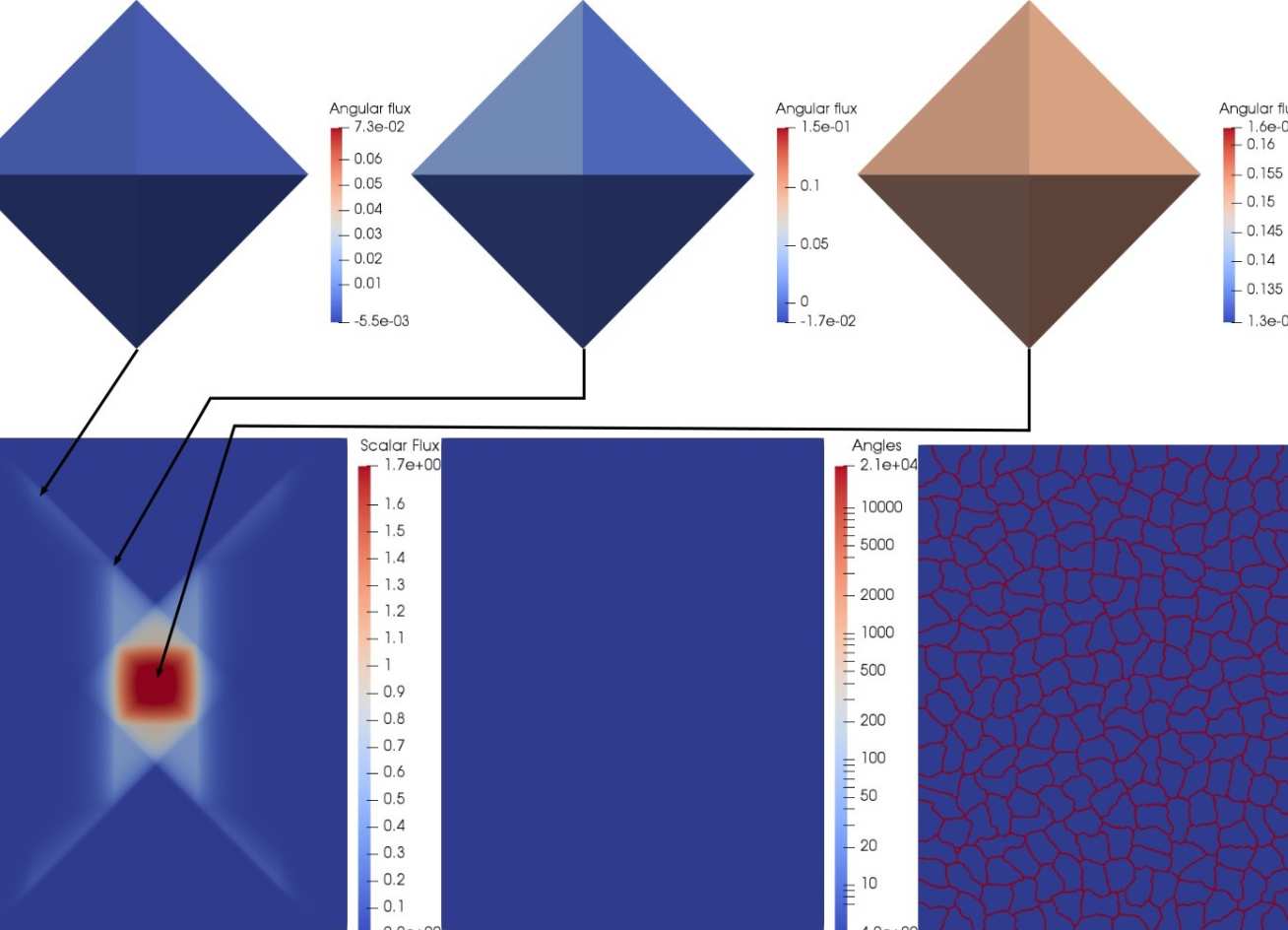
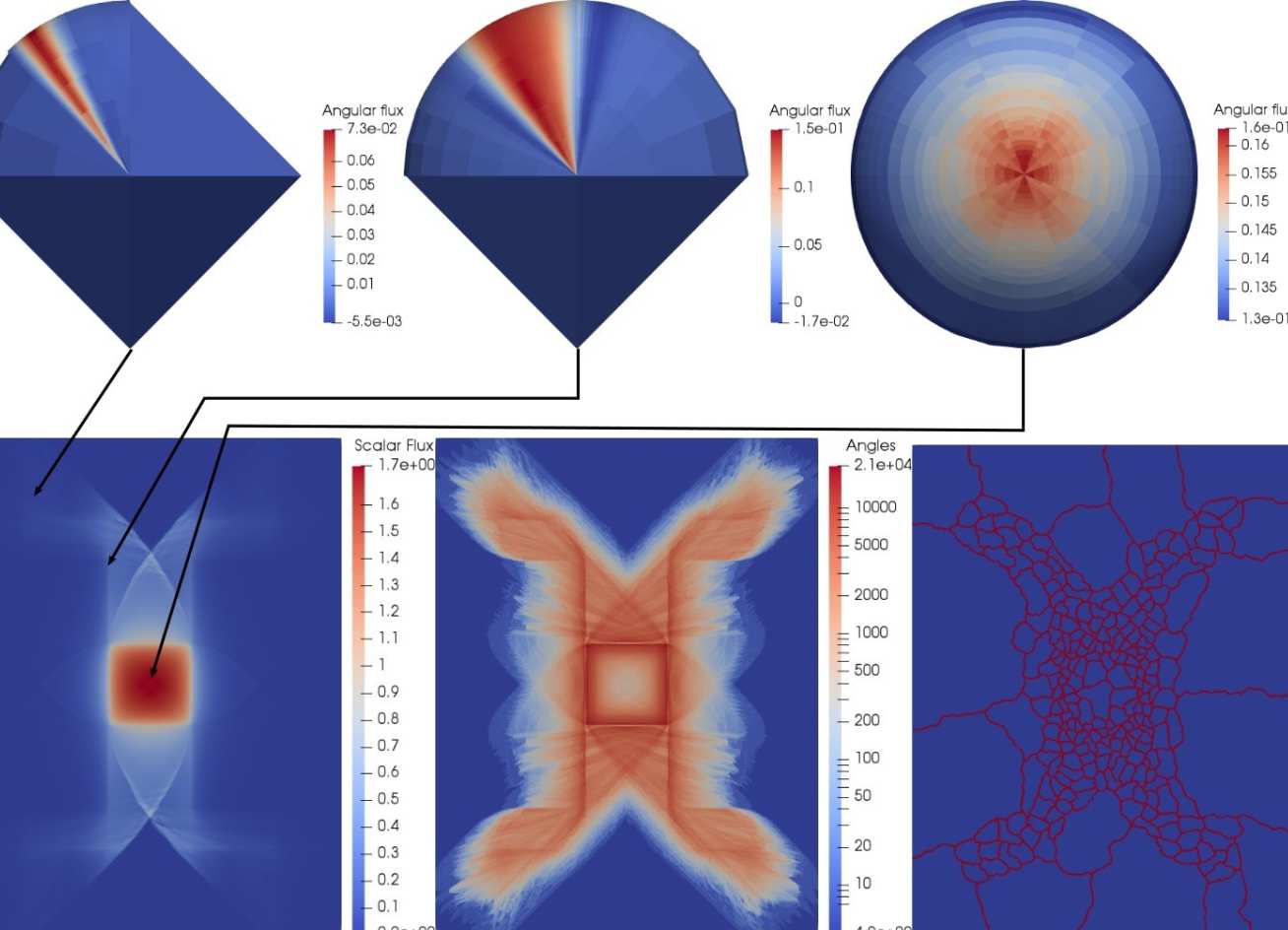
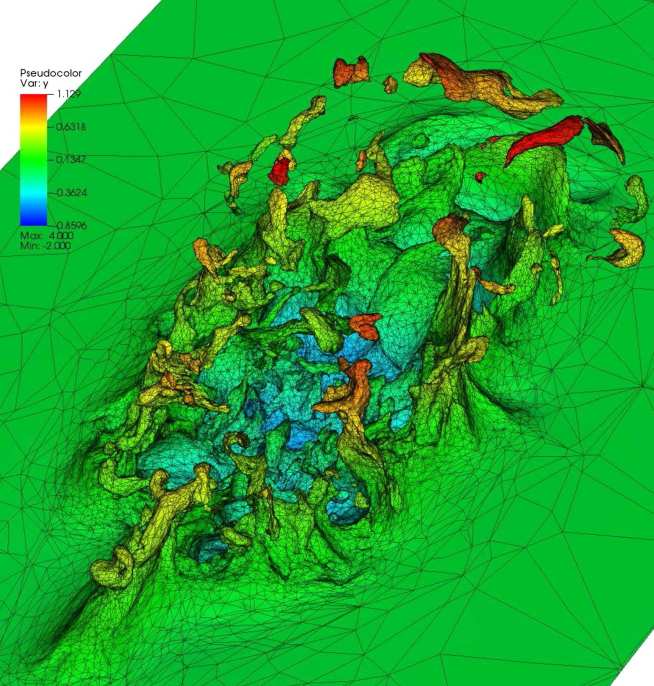
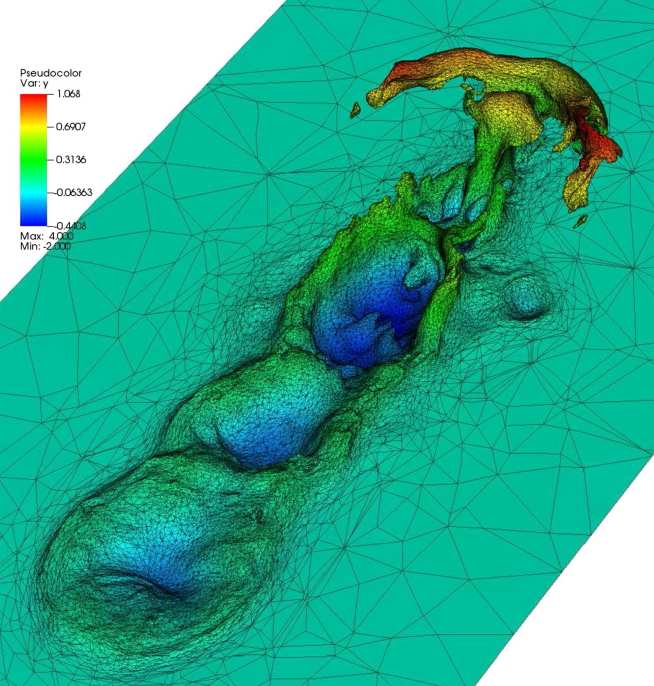
- The wavelet angular discretisations can adapt anisotropically on the sphere, differently at each point in space, allowing unprecedented accuracy in highly directional problems that require small solid angle to resolve (see Figures 1 & 2)
- Regular and goal-based adaptive schemes (see Figures 3-5) that can focus space/angle resolution only where important in an application
- Suitable for use in shielding, reactor-physics and criticality applications
- Sweep-free, matrix-free, space/angle multigrid methods on unstructured spatial grids provides flexibility for the FETCH2 framework
- Large-scale parallelism on modern HPC architectures
- Reduced order modelling capabilities for very rapid surrogate solutions
- The FETCH2 framework has also been extended into other Boltzmann applications, including radiative transfer, spectral-wave, Lattice-Boltzmann and kinetic modelling.
Continuing development of the FETCH2 framework is based around improving these numerical methods and applying them in a range of multi-physics applications, both in the nuclear field and more broadly. This includes the potential to couple to other codes in the AMCG, with the ambition of allowing coupled multi-phase CFD (see Figures 6 & 7) and “full physics” solid-fluids-radiation coupling.

FETCH
The motivation for the original FETCH framework comes from the potential for criticality where fissile materials are present in industrial or environmental applications, and from the associated need to assess the implications for the integrity of industrial plant and potential radiation impacts on the health of workers and the public. In general these applications will be multiphase, for example bubbly solutions, wetted or suspended powders or porous media.
While simple-design criticality assessment methods may normally be applied in a conservative manner, there is a need for a generic, fundamentally-based method capable of treating spatial and temporal detail, that may be used as a reference method and be used to assist in understanding complex behaviour. It is to meet this need that the coupled neutronics/CFD code FETCH (Finite Element Transient Criticality) has been developed and benchmarked against available experiments.
The code has been developed as a reference method for modelling criticality transients in fissile solutions and other multiphase matrices. The fundamental nature of the modelling means that the code may be applied to cases somewhat beyond the range of experiment - for example dilute plutonium solution transients.
Transient criticality has been the subject of active investigation in the last 20 years with encouraging results. The CRITEX code by Mather et al. was written to simulate the four important parameters of thermal expansion, temperature, radiolytic gas release and water vapour release, using point kinetics with cylindrical tank buckling and analytical treatments of the main variables. It has been validated against the CRAC and SILENE experiments. Later work led to the CHAMPAGNE treatment for high rates of reactivity addition in the presence of gas bubble formation. The related POWDER code, designed to simulate the ingress of a moderator into fissile powder, was developed following specific experiments using the SILENE reactor.
The time variation of power in fissile solution criticality depends on the means of addition of reactivity, the nature of the solution and the boundary conditions. In the case of a step reactivity addition, an initial rapid rise in power is (for uranium and concentrated plutonium solutions) terminated largely by nuclear temperature and density feedback; the subsequent fall in power is accelerated by evolution of radiolytic gas bubbles - which also pressurizes the solution. Since the rate of gas production, in the form of bubbles in the solution, effects the rate of fall of fission rate it can have a dominant role in determining the total yield in a short (a few seconds) excursion.
The approach to an approximately critical state may exhibit oscillations due to over expansion and contraction of the rising gas volume, sloshing of the free surface and, on a longer time-scale, due to the positive feedback of heat losses from the vessel. This asymptotic critical power is that which maintains solution conditions such that heat generation matches heat losses. In the case of continuous filling of a vessel, the magnitude of the initial power peak depends on the filling rate, and this is followed by successive power peaks as long as the filling continues.
It may be noted that, for dilute plutonium solutions (of the order 10 g/l), nuclear plus density reactivity feedback is positive and modelling demonstrates a different behaviour in that termination of the first power peak is only by gas evolution and the feedback from vessel heat losses is negative.
Compressibility has various influences on fluid behaviour; one example is the generation of pressure waves which propagate through a fluid with a characteristic velocity, related to the speed of sound. In addition, oscillatory behaviour often arises in internal flows, associated with compressibility, due to the spring-like nature of the pressure feedback from density changes. Transient behaviour of a solution is sensitive to the rate at which radiolytic gas may escape from a tank and suppression of radiolytic gas bubbles due to over-pressure and the pressure in the dynamically evolving liquid. Therefore it is important to take into account the role of pressure/compressibility in modelling the excursions.
Hetrick and Kimpland were the first to attempt to model pressure effects in criticality transients through the development of a multi-regional model. For each region, hydrodynamic models, for energy, continuity, and simplified momentum equations were enforced and coupled to a simple scalar equation providing the reactivity whose coefficients were obtained 'off-line' through transport calculations. These models were able to predict pressure traces and power in fissile liquids with gas production from the SILENE reactor with good accuracy.
Recent research has resulted in the incorporation of compressibility effects into the multiphase fluid modelling with FETCH. Taking into account pressure improves the accuracy of the modelling and provides valuable information about the forces exerted on the containment vessel(s) during a criticality excursion. The multiphase modelling was designed to represent bubble rise and bursting and the accompanying free surface motion, in the context of transient finite element modelling of buoyancy/pressure-driven fluid behaviour. Here we describe multiphase modelling of pressure/shock waves and show how this has helped clarify the role of radiolytic gas bubbles in pressurising a solution. The model is validated against the relevant SILENE experimental results.
With the incorporation of pressure effects in to FETCH there has been a realization that the high-frequency oscillations in pressure and fission rate, which often accompany an excursion, are due to spring-like oscillations in the radiolytic gas volume. This elastic behaviour has lead to the development of simple spring models.
Selected references for technology developed/used by the FETCH2 and original FETCH frameworks:
Radiation transport:
S. Dargaville, A. G. Buchan, R. P. Smedley-Stevenson, P. N. Smith, C. C. Pain, Scalable angular adaptivity for Boltzmann transport, Journal of Computational Physics 406 (2020) 109124.
S. Dargaville, A. G. Buchan, R. P. Smedley-Stevenson, P. N. Smith, C. C. Pain, Angular adaptivity with spherical harmonics for Boltzmann transport, Journal of Computational Physics 397 (2019) 108846.
A.G. Buchan, S. Dargaville, C.C. Pain, A combined immersed body and adaptive mesh method for simulating neutron transport within complex structures (2019), Annals of Nuclear Energy, 134: 88-100
M. A. Goffin, A. G. Buchan, S. Dargaville, C. C. Pain, P. N. Smith, R. P. Smedley-Stevenson, Goal-based angular adaptivity applied to a wavelet-based discretisation of the neutral particle transport equation, Journal of Computational Physics 281 (2015) 1032–1062.
M. A. Goffin, A. G. Buchan, A. C. Belme, C. C. Pain, M. D. Eaton, P. N. Smith, R. P. Smedley-Stevenson, Goal-based angular adaptivity applied to the spherical harmonics discretisation of the neutral particle transport equation, Ann. Nucl. Energy 71 (2014) 60–80.
M.A. Goffin, C.M.J. Baker, A.G. Buchan, C.C. Pain, M.D. Eaton, P.N. Smith, Minimising the error in eigenvalue calculations involving the Boltzmann transport equation using goal-based adaptivity on unstructured meshes (2013), Journal of Computational Physics, 242: 726-752,
A.G. Buchan, C.C. Pain, A.P. Umpleby, R.P. Smedley Stevenson, A sub-grid scale finite element agglomeration multigrid method with application to the Boltzmann transport equation (2012), International Journal for Numerical Methods in Engineering, 92, 3: 318-342
A. G. Buchan, A. S. Candy, S. R. Merton, C. C. Pain, J. I. Hadi, M. D. Eaton, A. J. H. Goddard, R. P. Smedley-Stevenson, G. J. Pearce, The inner-element subgrid scale finite element method for the boltzmann transport equation, Nuclear science and engineering 164 (2010) 105–121.
Coupled single-phase CFD and radiation:
L. Soucasse, S. Dargaville, A. G. Buchan, C. C. Pain, A goal-based angular adaptivity method for thermal radiation modelling in non grey media, Journal of Quantitative Spectroscopy and Radiative Transfer 200 (2017) 215–224.
Reduced order modelling:
L. Soucasse, A.G. Buchan, S. Dargaville, C.C. Pain, An angular reduced order model for radiative transfer in non grey media (2019), Journal of Quantitative Spectroscopy and Radiative Transfer,
229: 23-32,
A.G. Buchan, A.A. Calloo, M.G. Goffin, S. Dargaville, F. Fang, C.C. Pain, I.M. Navon, A POD reduced order model for resolving angular direction in neutron/photon transport problems, Journal of Computational Physics (2015), 296: 138-157,
Single and multi-phase CFD papers:
Lei, Q., Xie, Z., Pavlidis, D., Salinas, P., Veltin, J., Matar, O. K., ... & Jackson, M. D. (2018). The shape and motion of gas bubbles in a liquid flowing through a thin annulus. Journal of Fluid Mechanics, 855, 1017-1039.
Xie, Z., Hewitt, G. F., Pavlidis, D., Salinas, P., Pain, C. C., & Matar, O. K. (2017). Numerical study of three-dimensional droplet impact on a flowing liquid film in annular two-phase flow. Chemical Engineering Science, 166, 303-312.
Gomes, J. L. M. A., Pavlidis, D., Salinas, P., Xie, Z., Percival, J. R., Melnikova, Y., & Jackson, M. D. (2017). A force‐balanced control volume finite element method for multi‐phase porous media flow modelling. International Journal for Numerical Methods in Fluids, 83(5), 431-445.
Chicago
Pavlidis, D., Gomes, J. L., Xie, Z., Percival, J. R., Pain, C. C., & Matar, O. K. (2016). Compressive advection and multi‐component methods for interface‐capturing. International Journal for Numerical Methods in Fluids, 80(4), 256-282.
Fluid structure papers:
Yang P, Xiang J, Fang F, Pavlidis D, Pain CC, 2019, Modelling of fluid-structure interaction for moderate Reynolds number flows using an immersed-body method, Computers & Fluids, 2019 Jan 30; 179: 613-631.
Yang P, Xiang J, Fang F, Pain CC, 2019, A fidelity fluid-structure interaction model for vertical axis tidal turbines in turbulence, Applied Energy, 2019 Feb 15; 236: 465-477
Xiao D, Yang P, Fang F, Xiang J, Pain CC, Navon IM, Chen M, 2017, A non-intrusive reduced-order model for compressible fluid and fractured solid coupling and its application to blasting, Journal of Computational Physics, 330, 221-244
Yang P, Xiang J, Chen M, Fang F, Pavlidis D, Latham J-P, Pain CC, 2017, The immersed-body gas-solid interaction model for blast analysis in fractured solid media, International Journal of Rock Mechanics and Mining Sciences, 91, 119-132
Yang P, Xiang J, Fang F, Pavlidis D, Latham J-P, Pain CC, 2016, Modelling of fluid–structure interaction with multiphase viscous flows using an immersed-body method, Journal of Computational Physics, 321, 571-592
Xiao D, Yang P, Fang F, Xiang J, Pain C C, and Navon I M, 2016, Non-intrusive reduced order modeling of fluid-structure interactions. Computer Methods in Applied Mechanics and Engineering, 303, 35–54
Viré A, Xiang J and Pain C, 2015, An immersed shell method for modeling fluid structure interactions in aerodynamics, Philosophical Transactions A, Volume: 373 Issue: 2039.
Use of the original FETCH framework:
J.L.M.A. Gomes, C.C. Pain, M.D. Eaton, B. Tollit, A.J.H. Goddard, M.D. Piggott, A.K. Ziver, Y. Yamane (2011) "Coupled neutronics-fluids modelling of criticality within a MOX powder system", Progress in Nuclear Energy. 53(5):523-552.
B.E. Miles, C.C. Pain, J.L.M.A. Gomes, B. Tollit (2010) "Simulation of a gas-cooled fluidized bed nuclear reactor. Part I: Mixed oxide fuels", Annals of Nuclear Energy. 37(7):999-1013.
B.E. Miles, C.C. Pain, J.L.M.A. Gomes (2010) "Simulation of a gas-cooled fluidized bed nuclear reactor – Part II: Stability of a fluidized bed reactor with mixed oxide fuels", Annals of Nuclear Energy. 37(7)1014-1025.
J.L.M.A. Gomes, C.C. Pain, M.D. Eaton, A.J.H. Goddard, M.D. Piggott, A.K. Ziver, C.R.E. de Oliveira, Y. Yamane (2008) "Investigation of nuclear criticality within a powder using coupled neutronics and thermofluids". Annals of Nuclear Energy. 35(11):2073-2092.
J.L.M.A. Gomes, C.C. Pain, C.R.E. Oliveira, A.J.H. Goddard (2007) "A Numerical Investigation of Heat Transfer Mechanisms in Gas-Solid Fluidized Beds using the TFGTM", Heat Transfer Engineering 28:576-597.
D.Lathouwers, T.H.J.J.V.D Hagen, A. Agung, A.V. Damn, C.C. Pain, C.R.E. Oliveira, M.D. Eaton, A.J.H. Goddard, J.L.M.A. Gomes (2006) "On an improved design of a fluidized bed nuclear reactor - I: design modifications and steady-state features", Nuclear Technology 153:117-131.
C.C. Pain, J.L.M.A. Gomes, M.D. Eaton, C.R.E. Oliveira, A.J.H. Goddard, A.P. Umpleby (2005) "A Model of Heat Transfer Dynamics of Coupled Multiphase-Flow and Neutron-Radiation: Application to a Nuclear Fluidized Bed Reactor", International Journal of Numerical Methods for Heat and Fluid Flow 15:765-807.
C.C. Pain, J.L.M.A. Gomes, M.D. Eaton, C.R.E. Oliveira, A.J.H. Goddard, A.P. Umpleby, D.Lathouwers, T.H.J.J.V.D Hagen, A. Agung, A.V. Damn (2003) " Space-dependent kinetics simulation of a gas-cooled fluidized bed nuclear reactor", Nuclear Engineering and Design 219:225-245.
C.C. Pain, C.R.E. Oliveira, A.J.H. Goddard, M.D. Eaton, S. Gundry, A.P. Umpleby (2003) "Transient analysis and dosimetry of the Tokaimura criticality incident", Nuclear Technology 144:16-33.
C.C. Pain, J.L.M.A. Gomes, M.D. Eaton, C.R.E. Oliveira, K. Ziver, R.T. Ackroyd, B. Miles, A.J.H. Goddard (2002) "An investigation of power stabilization and space-dependent dynamcis of a nuclear fluidized-bed reactor", Nuclear Science and Engineering 144:242-257
C.C. Pain, S. Mansoorzadeh, J.L.M.A. Gomes, C.R.E. Oliveira, A.J.H. Goddard (2002) "A Numerical Investigation of Bubbling Gas-Solid Fluidized Bed Dynamics in 2-D Geometries", Powder Technology 128:56-77.
C.C. Pain, C.R.E. Oliveira, A.J.H. Goddard, A.P. Umpleby (2001) "Criticality behavior of dilute plutonium solutions", Nuclear Technology 135:194-215.
C.C. Pain, C.R.E. Oliveira, A.J.H. Goddard, A.P. Umpleby (2001) "Transient criticality in fissile solutions - Compressibility effects", Nuclear Science and Technology 138:78-95.
C.C. Pain, C.R.E. Oliveira, A.J.H. Goddard, A.P. Umpleby (2001) "Non-linear space-dependent kinetics for the criticality assessment of fissile solutions", Progress in Nuclear Energy 39;53-114.
C.C. Pain, S. Mansoorzadeh. C.R.E. Oliveira (2001) "Numerical modelling of gas-solid fluidized beds using the two-fluid approach", International Journal for Numerical Methods in Fluids 36:91-124.
C.C. Pain, S. Mansoorzadeh. C.R.E. Oliveira (2001) "A study of bubbling and slugging fluidised beds using the two-fluid granular temperature model", International Journal for Multiphase Flow 27:527-551.
C.C. Pain, C.R.E. Oliveira, A.J.H. Goddard (2001) "Transient Simulations of the Tokai-Mura Criticality Accident", Journal of the British Nuclear Energy Society 67:45-54.
C.C. Pain, A.J.H. Goddard (2000) "Insights into prolonged solution criticality incidents, using the coupled radiation/multiphase code FETCH", Nuclear Energy 39:381-385.