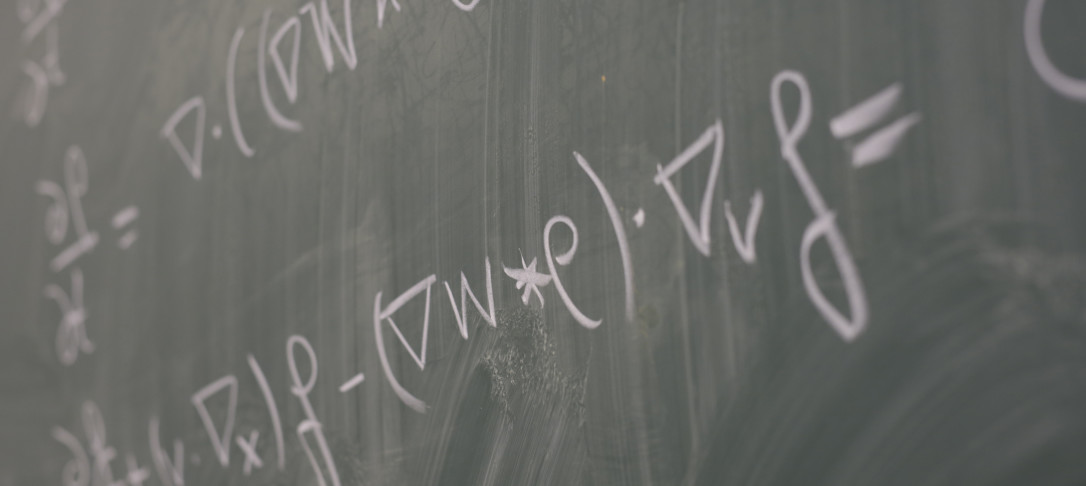
Title
Anomalous Regularization in Kazantsev-Kraichnan Model
Abstract
In this talk, we will investigate a passive vector field which is transported and stretched by a divergence-free Gaussian velocity field, delta-correlated in time and poorly correlated in space (spatially nonsmooth). Although the advection of a scalar field (Kraichnan’s passive scalar model) is known to enjoy regularizing properties, the potentially competing stretching term in vector advection may induce singularity formation. We will see that the regularization effect is actually retained in certain regimes. While this is true in any dimension $d\ge 3$, it implies a regularization result for linearized 3D Euler equations with stochastic modeling of turbulent velocities, and for the induction equation in magnetohydrodynamic turbulence.
The presentation is based on a joint work with Francesco Grotto and Mario Maurelli.
Please note that the seminar will take place in person in room 144 of Huxley Building.