Introduction
Cortexica was founded as a visual search company in 2008. Since its founding, I have often been asked to explain how its technology worked. Just over 5 years ago, it would have been difficult to describe the core technology of Cortexica: the Generic Vision Platform (GVP). The vocabulary that we used within the company borrowed terms from computational neuroscience and signal processing. In the absence of a shared vocabulary with those outside the company, we (myself and Jeffrey Ng, cofounders) used the relatively popular terminology of computer vision to explain some of the core algorithms that got the company off the ground.
 Figure 1. This 2008 version of the GVP illustrates one level of Cortexica’s planned architecture. Layers occur in pairs, and are all consist of spatial convolutions with linear and non-linear activations. See also Figure 3, which shows the original architecture in a more up-to-date depiction.
Figure 1. This 2008 version of the GVP illustrates one level of Cortexica’s planned architecture. Layers occur in pairs, and are all consist of spatial convolutions with linear and non-linear activations. See also Figure 3, which shows the original architecture in a more up-to-date depiction.
Since the success of AlexNet, the architecture of convolutional networks has come to have very wide impact, and part of a widely used technical vocabulary. Cortexica has always used such structures in its GVP, but with a few notable differences. These include:
- Using divisive normalisation rather than explicit activation functions
- Creating shared convolutional weights without the use of backpropagation
- Using weight adaptation through recurrent computations
- Using repeated pairs of convolutional layers, rather than single layers in cascade
Moving forward to today, Cortexica does indeed use backpropagation, or techniques from sparse-coding, to train networks to do specific tasks in vision, and will often use a variety of network architectures. These networks sit alongside the original GVP.
The Original Weight Set
We did not (in 2008) use backpropagation in the training of our original weight set. Instead, our weights were set using simple layer-wise optimisation. We also used weight constraints based on spatial symmetry and semi-analytic parametric functions, ideas that had been used in neuroscience and signal processing for decades. To understand this a bit better, look at Figure 2, which depicts the appearance of shared convolutional weights used within one of the layers of our network. The dark and light areas — as for standard convolutional units — are meant to represent positive and negative weights over a small patch of image space. As for standard convolutional units, these are repeated over space. However, as Figure 2 suggests, we can group the weight patterns into symmetric and antisymmetric pairs, and into 8 orientations. We used this weight arrangement in the design of the original GVP. The descriptions of the weight-patterns were created by polar separable functions in the discrete Fourier domain. The principles behind this design use three key ideas:
- Phase quadrature (a concept from communications and signal processing)
- Spatial frequency characteristics of biological neurons in mammalian visual systems (area V1)
- Frame properties (a concept from signal processing and discrete mathematics).
 Figure 2. A simplified depiction of the symmetries and directions used in 4 layers of Cortexica’s first convolutional network (2008). The symmetry and directions of the weight patterns are designed so that they are adaptive; they are designed — in combination — to reproduce the linear effect of a much larger set of shared weights. Weights may be grouped into channels of orientation, two classes of symmetry and a variety of spatial scales.
Figure 2. A simplified depiction of the symmetries and directions used in 4 layers of Cortexica’s first convolutional network (2008). The symmetry and directions of the weight patterns are designed so that they are adaptive; they are designed — in combination — to reproduce the linear effect of a much larger set of shared weights. Weights may be grouped into channels of orientation, two classes of symmetry and a variety of spatial scales.
One group of weights may be grouped into 8 channels of orientation, two classes of symmetry and a variety of spatial scales. This diagram shows only 4 pairs of weights belonging to 4 channels; another 4 pairs are present, completing the circular arrangement; we don’t show them because their explicit covolution with the image is redundant.
We’ll discuss the importance of this arrangement of weights a bit more in the next section. But in essence, this relatively small number of weights allows almost infinite weight variability through the principle of steerability (weight adaptation). The total number of CNN-equivalent weight values to be specified for a single layer is 3,600. The effective weight set under adaptation is infinite (to machine precision).
The weights of the set, shown in Figure 2, all share the property that – when applied over a patch – they provide maximum positive or negative weighting to pixels within the centre of the patch (whatever stride is used). A second weight set (not shown) is used. The second weight-set provides maximum weighting off centre to the patch it is applied to. This second weight set is applied by spatial convolution as well, but there is a strongly non-linear function between the outputs of first and second layer weights.
Finally, the weights were also designed — when used in a many-layered convolutional network — to provide a nearly complete description of the input image. That is, the outputs of all layers of the network produce a representation or encoding of the input that can be linearly reconstructed to a high degree of accuracy (frame tightness property). This was the principle used to design a single layer of this weight set. We also used principles from multirate filtering. Mathematically, the spatial kernel that implicitly generates our multiscale representation is a Poisson kernel, rather than a Gaussian.
The Architecture of the GVP
Our original architecture for the GVP was developed between 2007 and 2008. In its initial form, it was not quite as deep as that of AlexNet and systems such as Inception. The depth of training very deep networks hinges on the availability of “Big Data”. Big Data (for the usual purposes of training convolutional networks) means having not only many images, but also accurate labels if you are to train using standard back-prop. Large sets of labelled image data were not available to us at that time (with the exception of trivial data sets such as hand-writing and small images, such as CIFAR 10). We therefore fell back on signal processing and biology to come up with the structure of the network and the non-linear operation of divisive normalisation used between each pair of layers shown in Figure 3.
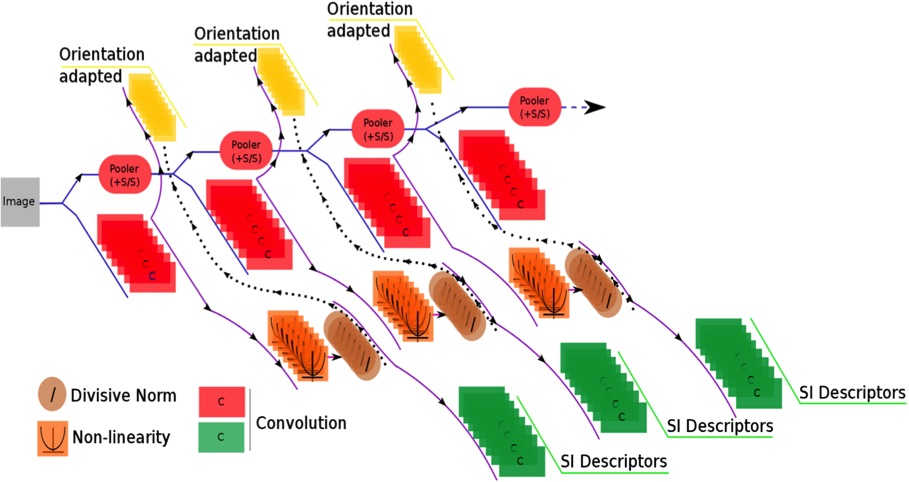 Figure 3. A representation of the main pipeline of the original GVP that was developed in 2008. The convolutional layers, non-linearities and recurrent connections are clearly visible. Later versions used many more layers. Note the layer pairs: red and green linear convolutional units. Note shown: we can also combine information from later layers back to earlier layers (not backprop, but at run-time). Note that the term “orientation adapted” is slightly misleading: whilst we initially used these recurrent connections to generate synthetic convolutional units with rotated weight patterns, we found that we could also synthesize a broad set of effective weight patterns through adaptation.
Figure 3. A representation of the main pipeline of the original GVP that was developed in 2008. The convolutional layers, non-linearities and recurrent connections are clearly visible. Later versions used many more layers. Note the layer pairs: red and green linear convolutional units. Note shown: we can also combine information from later layers back to earlier layers (not backprop, but at run-time). Note that the term “orientation adapted” is slightly misleading: whilst we initially used these recurrent connections to generate synthetic convolutional units with rotated weight patterns, we found that we could also synthesize a broad set of effective weight patterns through adaptation.
The resulting architecture might look simple or shallow by today’s standards. But it has some really good features. First, the effective convolution weights are adaptive in response to top down information. This is a form of recurrent computation in which the responses of the linear parts of convolutional units can be adjusted based on information computed elsewhere in the network.
For example, with a small number of orientations in our set of convolutional (shared) weights, we could synthesise “missing” orientations. The ability to synthesise linear responses of units to different convolution weight sets also applies to phase symmetry for a given orientation. Together, these two forms of adaptation mean that the effective weight set that can be applied to an incoming image is almost infinite.
Have a look at Figure 4. This shows how the weights of convolutional units may be synthesised by re-weighting the outputs of an input image consisting of a set of impulse functions spaced around the perimeter of a circle. To appreciate why the rightmost two panels represents “synthetic” weights, you need to appreciate how spikes in the image plane (known as delta functions – not shown) interact with linear systems, such as the linear part of a spatial convolutional unit.
 Figure 4. Adapted responses using the fixed weight sets illustrated in Figure 2; left, symmetric and right, antisymmetric. There are more oreintations of kernel present in this image than in the orinal limited set of 4 directions. The input image consists of a set of 12 impulses spaced around the perimeter of a circle.
Figure 4. Adapted responses using the fixed weight sets illustrated in Figure 2; left, symmetric and right, antisymmetric. There are more oreintations of kernel present in this image than in the orinal limited set of 4 directions. The input image consists of a set of 12 impulses spaced around the perimeter of a circle.
This adaptation extends beyond merely altering phase symmetry and orientation: we can — within the space of a single patch — vary the weighting that is applied. An example of this principle is illustrated in Figure 5.
 Figure 5. By reweighting the results of linear convolution units, the GVP architecture can generate responses to weights that are not actually in the layer. This is similar to the principle of steerable filters.
Figure 5. By reweighting the results of linear convolution units, the GVP architecture can generate responses to weights that are not actually in the layer. This is similar to the principle of steerable filters.
Invariance Through Symmetry
One can train networks of artificial neurons to learn to be invariant to shifts and rotations. One can also design such trivial invariance properties into weight sets. In an earlier part of this page, I mentioned the term quadrature. Mathematically, two functions of one variable that are in quadrature relationships have a 90 degree phase shift between them. Pairs of such quadrature functions have an automatic invariance (or approximate invariance) to shifts. Depending on whether the dependent variable of the function describes a linear or angular change in pattern either approximate rotational invariance and shift invariance can be designed into the weight sets.
Invariance itself is a double-edged sword. In some cases, I might want my neurons to be invariant to certain types of transformation. At other times, I want to be selective. Let’s take a trivial example in rotation invariance. Sometimes, I want to be able to get a neuron or complete network to detect an object or structure irrespective of its rotation relative to the image plane of a camera. At other times, I want to be able to sense the difference between something that is right-side up or not. It all depends on the nature of the task (in computer vision parlance). Often, I want to both detect a structure and know which way it is facing, or oriented. In order to achieve this, a little bit of good algorithm/feature design is helpful. So, the GVP was designed to facilitate either rotation-invariant or rotation-selective behaviour, as required.
Returning to quadrature: all the weight-sets of the main GVP use quadrature pairs of weights. Some are in linear quadrature, others in angular quadrature. There are further details available about the way that scale invariance is obtained, but that is another story.
Activation Functions
We do not use explicit activation functions in our initial GVP, but we planned that different non-linearities could be applied for different tasks. This, together with the adaptivity of the weight-set, means that there is very high flexibility built into the core GVP without the need for extensive training. For many of the calculations used for perceptual descriptors (you should talk to Cortexica about this for more details), we apply divisive normalisation to outputs, returning these separately to the linear responses. Divisive normalisation implicitly constrains the results of the linear convolution to behave in a non-linear fashion (the characteristic is like a saturating non-linearity). Unlike AlexNet, we grouped the convolutional units that are combined in divisive normalisation in a structured way. However, we had access to the raw linear outputs from the linear portions of the convolution calculation. Both linear and non-linear responses were simultaneously accessible at each level.
“Backprop” rules, OK ?
Although much of the GVPs early weight design work was based on semi-analytical or piecewise analytical functions, we used numeric optimisation in parametric space to work out good weight sets. However, it’s worth saying that if we were starting again, we’d probably simply design the weights of our stacked convolutional layers using backprop. This does not mean that there are not other ways to engineer really nice weight sets with really robust properties and minimal training. Backprop does involve significantly less work ! Today, Cortexica uses Backprop extensively, as do members of the BICI Lab.
Contact us
Prof Anil Anthony Bharath
a.bharath@imperial.ac.uk
Telephone
+44 (0)20 7594 5463
Address
Room 4.12
Department of Bioengineering
Royal School of Mines Building
Imperial College London
