resume

PhD Chemical Engineering, Imperial College London, UK (advisor: Serafim Kalliadasis); Diploma Mechanical Engineering, Technische Universität Darmstadt, Germany; MS Mathematics & Computing, Technische Universität Darmstadt, Germany.
About
Following Imperial position Andreas joined as a PDRA the Theory of Neural Dynamics, Max Planck Institute for Brain Research, Frankfurt, Germany. Now Senior Data Scientist, Computational Modeling & Software Engineering, DB Systel GmbH. The information below was of relevance whilst a PhD student in the Complex Multiscale Systems group.
I was a PhD student in the Complex Multiscale Systems group led by Professor Serafim Kalliadasis. Prior to this, I was a research and teaching assistant with Professor Martin Oberlack (TU Darmstadt), where I graduated in Mechanical Engineering (Diploma) and in Mathematics and Computer Science (BSc). My current PhD topic is Multiscale Analysis of a Moving Contact Line. What drives me in my research is the fascination of applying interdisciplinary approaches on physical problems, using a combination of modelling, numerical and analytical techniques.
Motivation
A raindrop sliding down the leaf of a tree seems to be one of the most ordinary physical phenomena one could think of. However, if we look a bit closer, what seemed so simple reveals to be of an unexpected complexity. Let us zoom into the line surrounding the drop, where the water, the air and the surface of the leaf meet. In this line, a relatively dense liquid pushes away a gas of a low density, and wets the solid leaf. While we can describe mathematically relatively well each of the phases – the solid, the gas and the liquid –, as well as their respective interfaces, bringing them all together in one point leads to a multitude of physical effects out of which many are still not fully understood. Interestingly, the generality of the phenomenon means that improving our understanding for the drop sliding down the leaf can help in the modelling and improvement of a broad range of technical applications.
Current Research
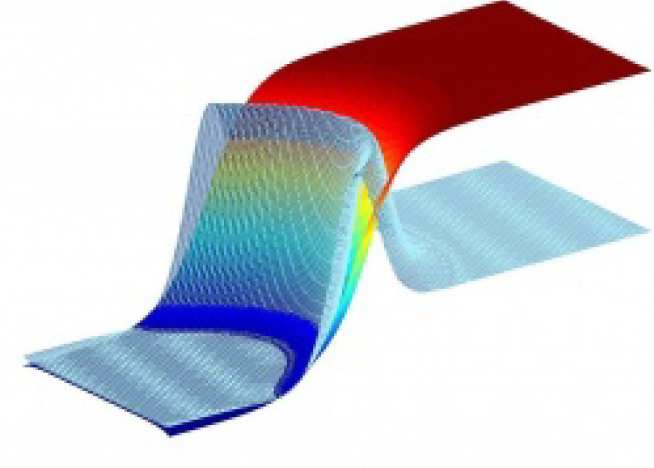
In my PhD, I study the phenomenon of a moving contact line, mainly using numerical schemes to solve diffuse interface approaches. This part of my research is closely interlinked with computations of equilibrium and dynamical colloidal systems using Density Functional Theory. My main interest is to use numerical schemes, in combination with asymptotic methods, to develop a better understanding of multiscale phenomena at the moving contact line.
I am also interested in the application of Symmetry methods on hydrodynamic stability problems. In particular, I am interested in how Lie-point symmetries can lead to reduced models for perturbations of laminar shear flows.