Graphs showing the shape of photocurrent kinetics and where the flat band potential is
Predicted effects of electrode potential on photocurrent densities according to the Gartner-Butler equation, and its modified versions that account for losses due to charge recombination, attenuation by reactor components and photon flux limitation

What is the flat band potential?

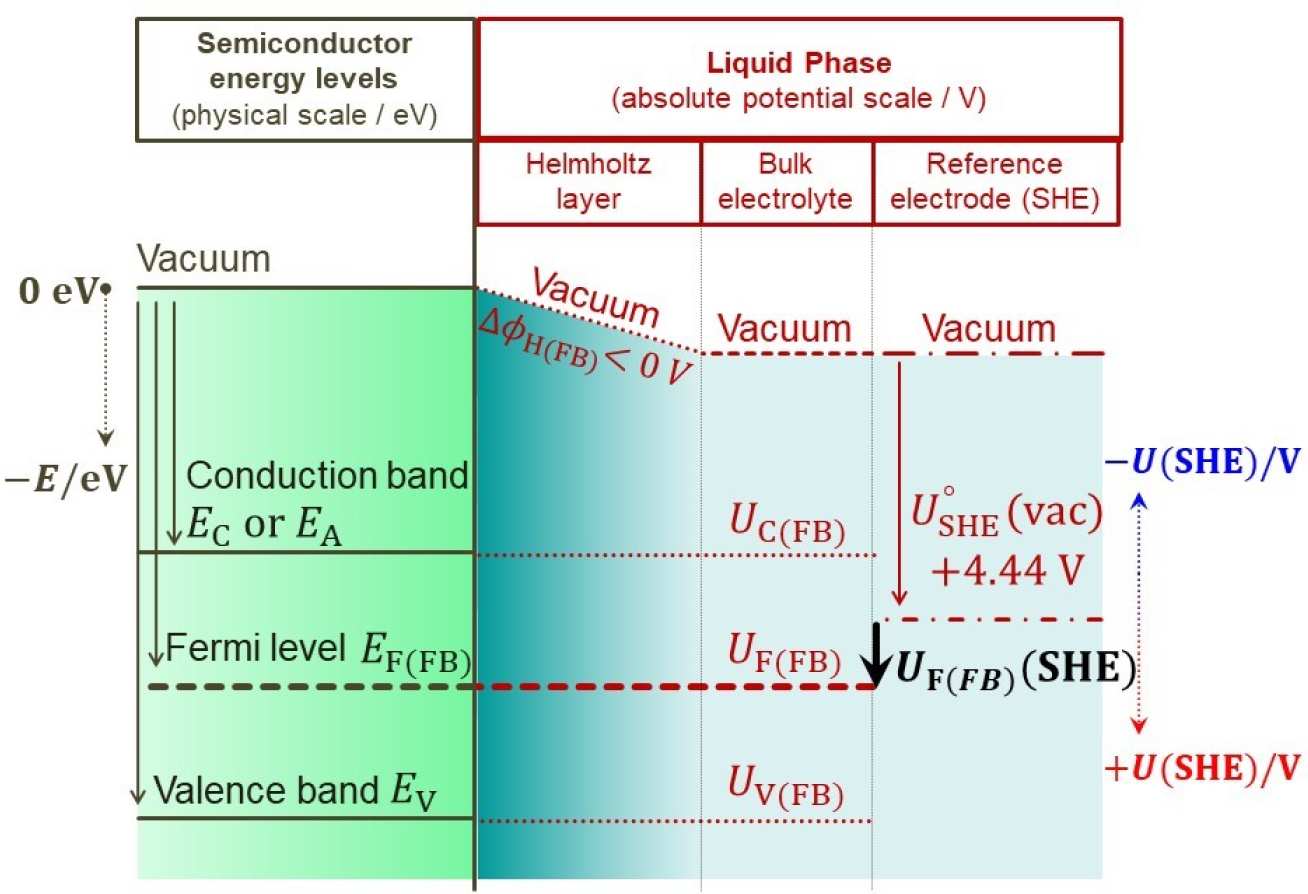
The term flat band refers to the condition when a semiconductor in contact with another material is not polarized in the interfacial region. At this condition, the conduction and valence bands are referred to as 'flat' and no electric field acts on the charge carriers. The flat band condition is a suitable and important reference state relative to which photoelectrochemical kinetics may be assessed (see illustrative grahs on the left). It is also the reference point of zero band bending, which is important in analysing the capacitance of the space charge layer. In summary, performances of photoelectrodes are dependent critically on their flat band potentials, as key material properties.

Why is the flat band potential such an elusive parameter?

Diagram showing alignment of energies between semiconductor and solution
Energy level diagram and corresponding potentials for an arbitrary semiconductor|electrolyte junction at the flat band condition, UF = UF(FB), and when the solution pH is greater than pH of point of zero charge of the electrode, pH

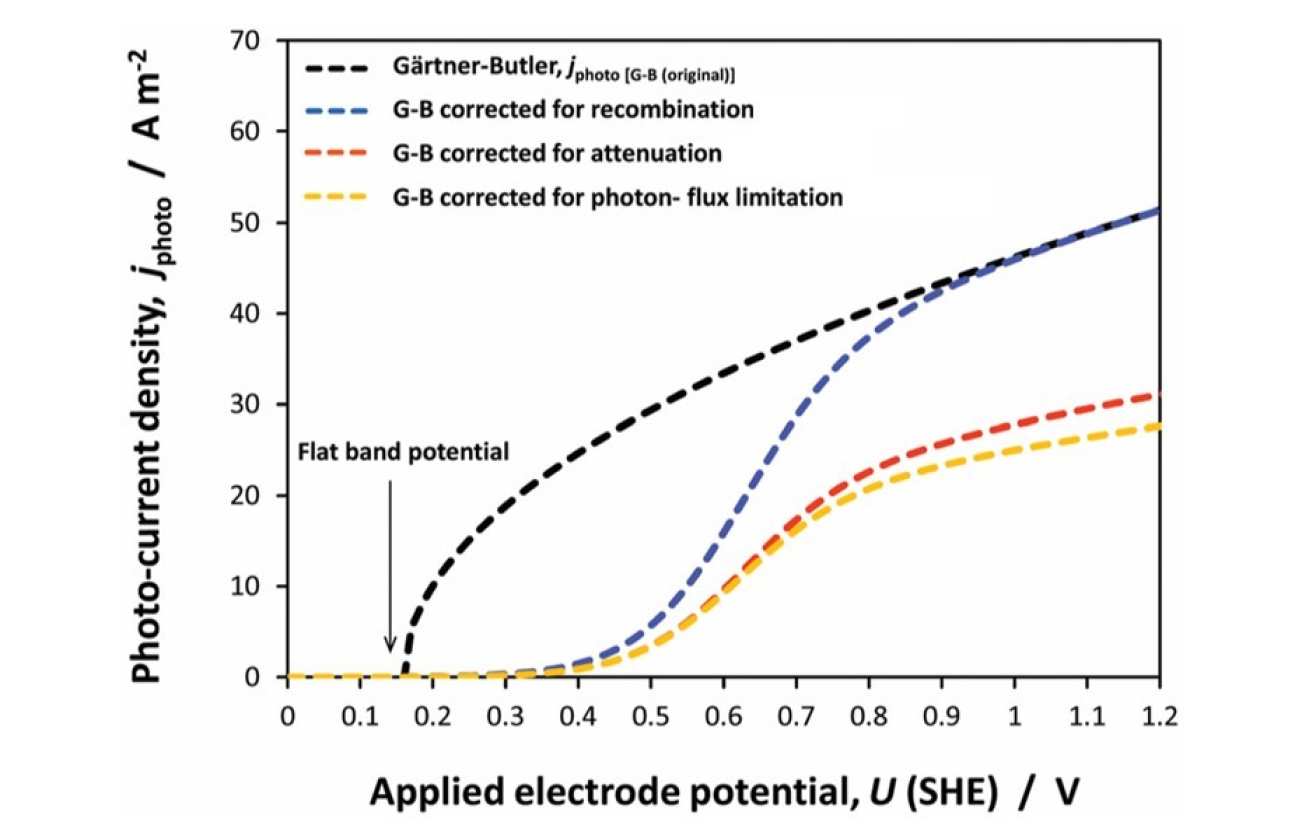
Using the example of synthetic hematite, we have shown that values of flat band potentials reported in the literature differ widely, and cannot be reconciled by differences in experimental conditions used in their determinations. The accuracy of flat band potentials is essential to model predictions of photoelectrochemical kinetics that may be used to understand mechanisms of rate controlling and loss processes, and for predicting performances of up-scaled photoelectrodes.

We have demonstrated through theory and experiments that different flat band potential determination methods can yield widely different results, so could mislead the analysis of the photoelectrode performance. We have examined extensively: (a) application of the Mott–Schottky (MS) equation to the interfacial capacitance, determined by electrochemical impedance spectroscopy as a function of electrode potential and potential perturbation frequency; (b) Gärtner–Butler (GB) analysis of the square of the photocurrent as a function of electrode potential; (c) determination of the potential of transition between cathodic and anodic photocurrents during slow potentiodynamic scans under chopped illumination (CI); (d) open circuit electrode potential (OCP) under high irradiance. Methods GB, CI and OCP were explored in absence and presence of H2O2 as hole scavenger. The CI method was found to give reproducible and the most accurate results on hematite but our overall conclusion and recommendation is that multiple methods should be employed for verifying a reported flat band potential.

Another critical aspect of semiconductor|liquid interfaces that needs to be accounted for is the presence of a potential drop across the Helmholtz layer; this drop is non-zero at all conditions except the pzc AND flat band. This drop results in an offset betweent the vacuum levels in the solid phase and in the solution phase (see schematic above) and is extremely important when mapping the energy alignment of a semiconductor material.

Publications