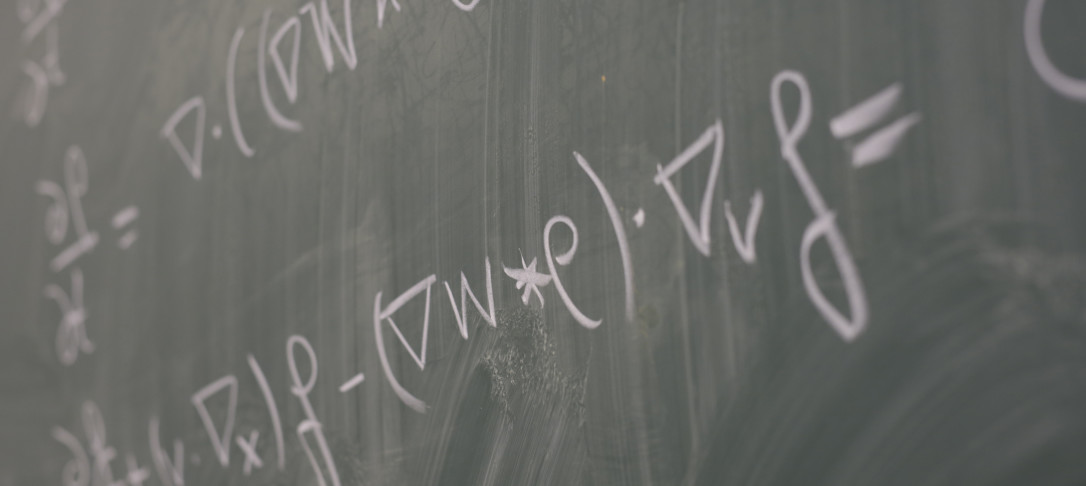
Title
Wave maps and mode stability of a blow up solution
Abstract
Wave maps are the hyperbolic analogue of harmonic maps and are the prototype of all geometric wave equations. I will introduce the wave maps equation and talk about specific examples arising naturally. I will then briefly discuss well-posedness theory which highlights one of the main features in the study of geometric wave equations: the intersection between analytical and geometric methods. Finally we will discuss a specific example of a blowup solution to the wave maps equations which is conjectured to describe generic blow-up behaviour and briefly discuss how to prove its mode stability.