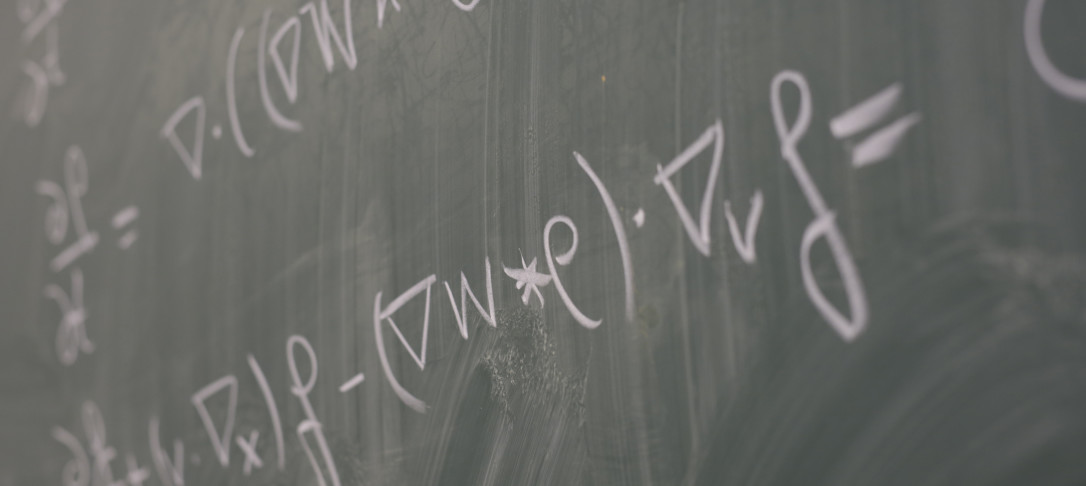
Title
Rigorous enclosure of the Lyapunov exponent for the Hopf Bifurcation with additive noise
Abstract
Recently, shear has been a much studied mechanism to induce chaos in random dynamical systems. This phenomenon is usually characterised by the positivity of the top Lyapunov exponent. In the Hopf normal form with additive noise, this Lyapunov exponent can be written as an integral over the solution of an associated Fokker-Planck equation. In this talk, I will give the sketch for a simple computer-assisted proof to enclose the solution of this PDE (and hence the Lyapunov exponent) for a finite shear parameter.
In the PDE context, computer-assisted proofs usually consist in combining tools from Functional and Numerical Analysis to rigorously enclose solutions of PDEs in a small neighbourhood of an approximation. Despite exploiting much of the structure of the problem, I will show that the PDE is barely not solvable but that this difficulty can be overcome.
Please note that the seminar will take place in person in room 140 of Huxley Building.