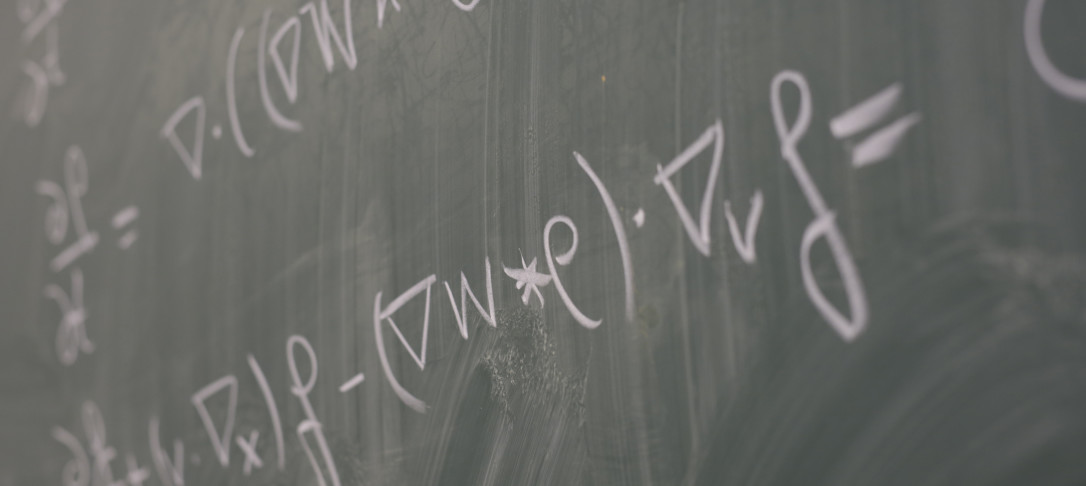
Title
Sub-exponential tails in biased run and tumble equations with unbounded velocities
Abstract
Run and tumble equations are widely used models for bacterial chemotaxis. In this talk, we present the long time behaviour of run and tumble equations with unbounded velocities. We show existence, uniqueness and quantitative convergence towards a steady state. In contrast to the bounded velocity case, the equilibrium has sub-exponential tails and we have sub-exponential rate of convergence to equilibrium. This produces additional technical challenges. We are able to successfully adapt both Harris’ type and L^2− hypocoercivity
Please note that the seminar will take place in person in room 144 of Huxley Building.