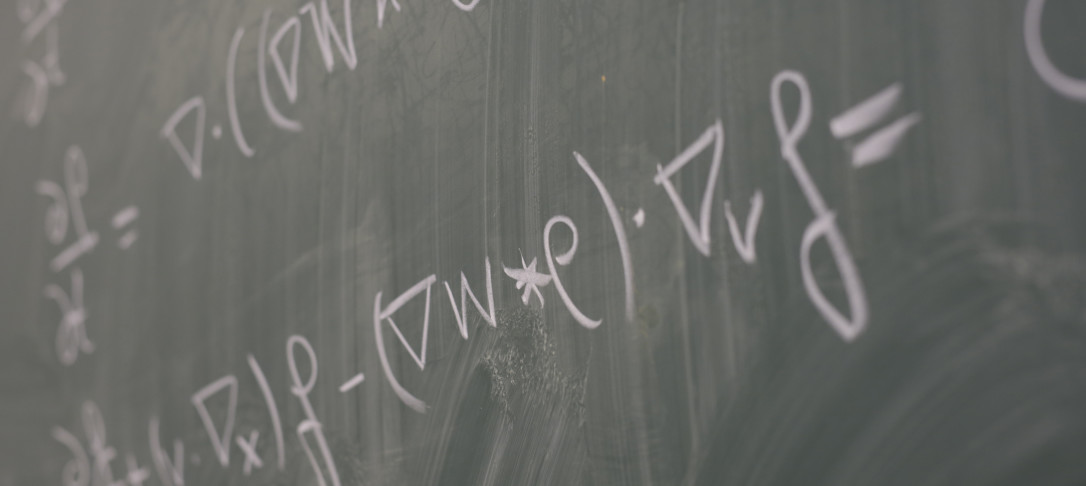
Title
Regularity of solutions to the Navier–Stokes equation with initial data in $\mathrm{BMO}^{-1}$
Abstract
A renowned work (Koch-Tataru, 2001) establishes small-data global existence of mild solutions to the Navier-Stokes equation in the endpoint critical space $\mathrm{BMO}^{-1}$. Later on, (Miura-Sawada, 2006) and (Germain-Pavlovic-Staffilani, 2007) obtain spatial analyticity of the Koch-Tataru solution. But time regularity remains unknown. In this talk, we address time regularity for all mild solutions in the Koch-Tataru solution class with initial data in $\mathrm{BMO}^{-1}$, as well as the long-time behavior of global ones.
Please note that the seminar will take place in person in room 144 of Huxley Building.