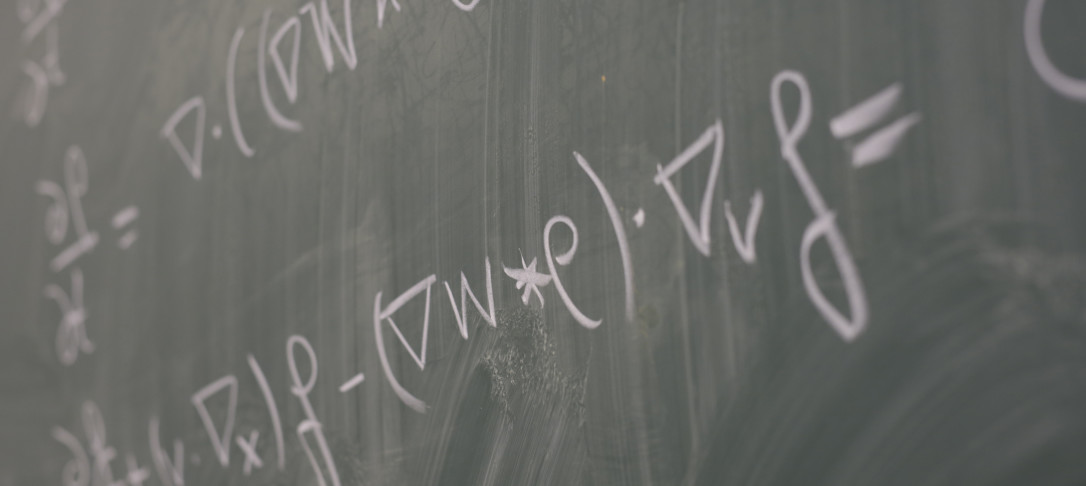
Title
Vanishing viscosity non-unique solutions to the forced 2D Euler Equations
Abstract
In the last decades, different techniques were developed to prove results around the topic of (non-)uniqueness of fluid dynamical PDEs. It is then an important question to understand if there is a selection principle for these equations, namely if such non-unique solutions can also be obtained in the limit of regularised problems (in which, for instance, a dissipative term is introduced: the vanishing viscosity limit). Remarkably, in the context of conservation laws, selection happens.
In a joint work with Dallas Albritton and Maria Colombo, we address this issue in the context of the forced 2D Euler equations, for which Vishik (2018) recently constructed non-unique solutions. We prove that the unique Leray solutions to the 2D Navier-Stokes system, forced with Vishik’s force and starting from a perturbation of Vishik’s initial datum, converge to a one-parameter family of solutions when we take the double limit of vanishing viscosity and perturbation size.
For the latter, we discover a uniqueness threshold below which the vanishing viscosity solution is unique and radial, and at which the viscous solutions converge to non-unique, non-radial solutions.
Please note that the seminar will take place in person in room 341 of Huxley Building.