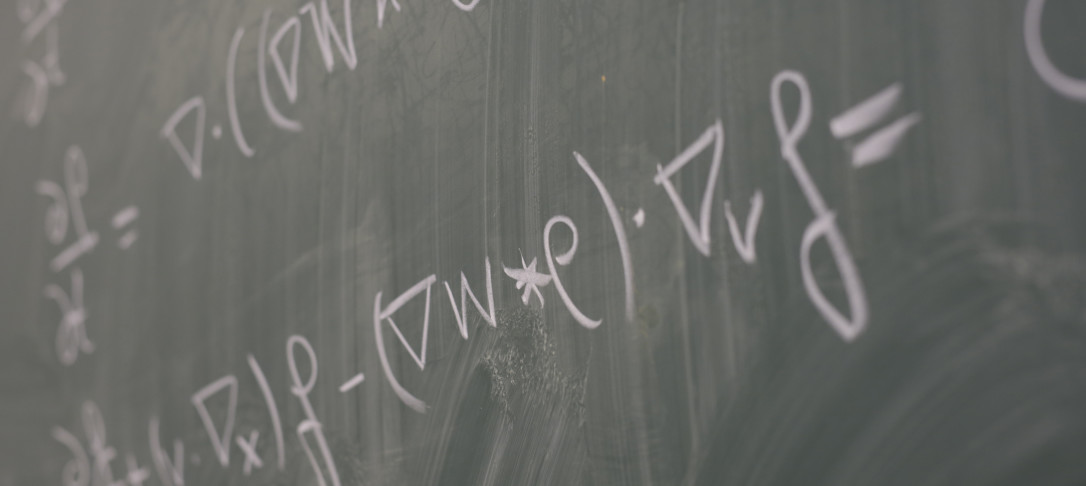
Title
Linear and non-linear wave equations in expanding spacetimes
Abstract
We discuss the geometric wave equation in a class of spacetimes that are homogeneous and isotropic, i.e. that approximately describe, at large scales, the universe we live in. While this hyperbolic PDE can be seen as a damped wave equation in Euclidean space (where the damping term is non-autonomous), its geometric interpretation in the theory of general relativity allows to associate dispersive properties of solutions to physical properties of the spacetime, such as its rate of expansion. In this context, we show that small data global existence holds for solutions to the Fritz John equation $\square_g \phi = (\partial_t \phi)^2$ even in case of decelerated expansion, due to the regularizing effects of the dynamical background. This is joint work with João Costa and Jesús Oliver.
Please note that the seminar will take place in person in room 140 of Huxley Building.