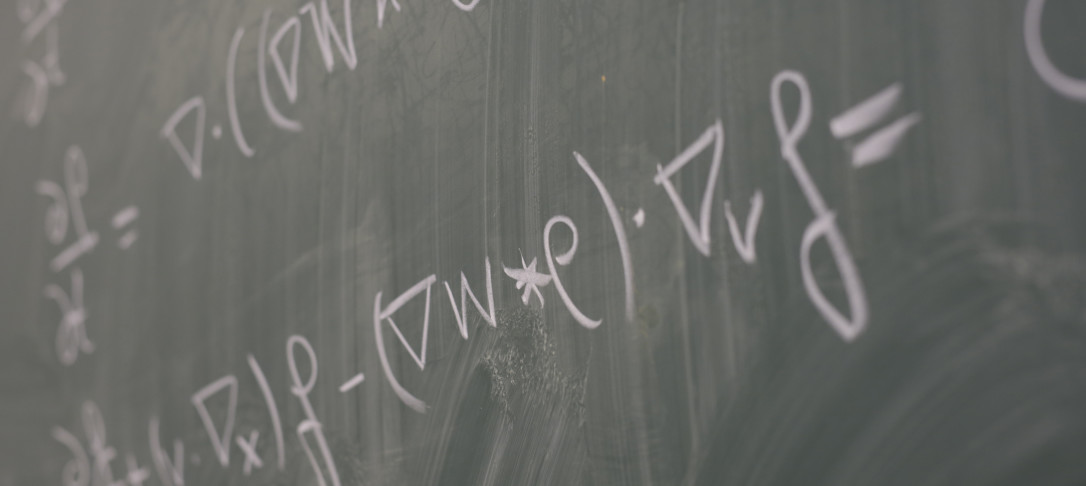
Title
Quantitative stability of the Rossby—Haurwitz waves of degree two for the Euler equations on the sphere.
Abstract
The motion of an incompressible, ideal fluid is described by the Euler equations. Choosing the unit sphere $\mathbb{S}^2$ embedded in $\mathbb{R}^3$ as the domain of interest, the Euler equations represent a suitable model for stratospheric flows. Among such flows, of particular importance in atmospheric dynamics are the Rossby—Haurwitz waves, that are observed in the stratosphere of the Earth and other planets, such as Jupiter, Saturn, Uranus, and Neptune.
In this joint work with Matias G. Delgadino (https://arxiv.org/abs/2509.16156), we show that the degree-2 Rossby—Haurwitz travelling waves on the Euler equations on $\mathbb{S}^2$ are orbitally stable. Our proof is short, quantitative, and conceptually easy to follow.
In this joint work with Matias G. Delgadino (https://arxiv.org/abs/2509.16156), we show that the degree-2 Rossby—Haurwitz travelling waves on the Euler equations on $\mathbb{S}^2$ are orbitally stable. Our proof is short, quantitative, and conceptually easy to follow.
Please note that the seminar will take place in person in room 140 of Huxley Building.