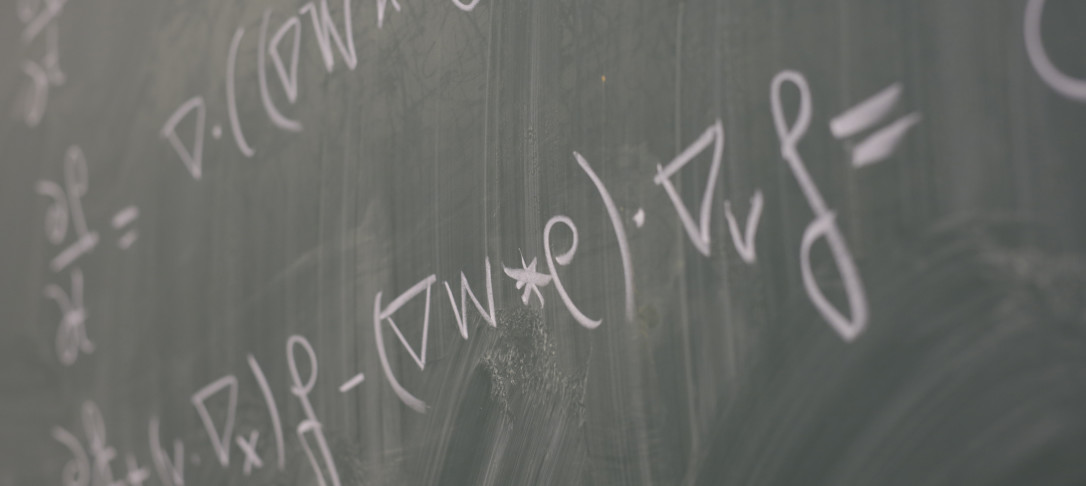
Title
Regularity of the density matrix for the Schrödinger equation applied to atoms and molecules
Abstract
By averaging over positions of all but one of the electrons, both the electron density and the density matrix are convenient objects to understand how electrons are distributed in space around an atom or molecule. It was previously proven that the electron density was smooth and real analytic away from the nuclei. We apply similar methods to show the same for the density matrix away from the nuclei and the diagonal. The lack of smoothness on the diagonal is interesting, and we study this further by considering the derivatives in the vicinity of the diagonal. We observe that the first four derivatives are bounded at the diagonal. This is joint work with my supervisor A.V. Sobolev.
Please note that the seminar will take place in person in room 413 of Huxley Building.