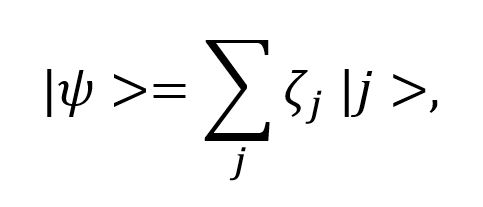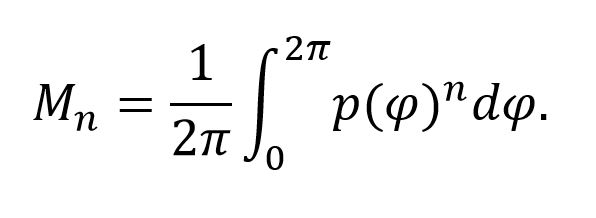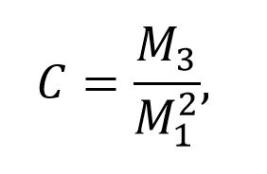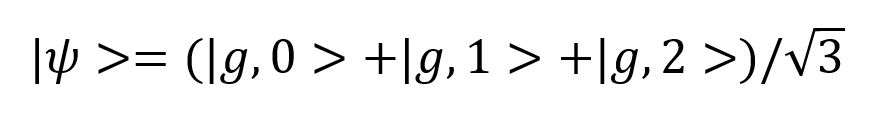Certifying Multilevel Coherence

A key feature of quantum mechanics is that systems can be in a superposition of their basis states. These coherent superpositions are responsible for many of the counter-intuitive predictions of quantum mechanics, such as in a double slit experiment where an interference pattern is seen due to each single particle being in a superposition of passing through each individual slit.

The ability to manipulate superpositions of quantum states underpins emerging quantum technologies such as quantum computing, and more generally studying the interference between states is of importance in investigations into the fundamentals of quantum mechanics.

The ability for a quantum particle to be in a coherent superposition of physical states is an important distinction between classical and quantum mechanics, and efforts to properly define and quantify this coherence are relatively recent [1, 2]. Determining if a quantum system truly is in a coherent superposition of states or if it is simply in a classical probabilistic mixture can be difficult, since such properties must be determined statistically by repeated measurements.

We can define a pure quantum state using the following formula,

where our quantum system is defined in terms of the basis states {|j>}, and is said to be k-coherent is there are at least k nonzero coefficients ζj.

The objective of our research is to define a coherence metric with single number that can be measured using a simple experiment. The certifier  used in our experiments is a function of normalised moments given by the expression,

For a probability distribution, the first moment is the expected value, with the third moment being the skewness of the distribution. Our certifier takes the ratio between these values[3],

which is able to overcome any measurement imperfection to prevent any over-estimates in the number of coherently superposed amplitudes[4]. Obtaining a value of C greater than 1 requires 2-coherence, greater than 5/4=1.25 requires 3-coherence, and greater than 179/96≈1.86 is necessary to certify 4-coherence in a Hilbert space of arbitrary dimention [3].

The motional states of a trapped ion provide the ideal system to demonstrate this certifier as each physical quanta of motion in the system is an oscillator Fock state . Without the ability to directly probe these states, we instead project the motional state onto the optical qubit of our ion using an interference pattern method. It is this probability distribution in which we apply our certifier .

In our experiment we use the axial motional states of a trapped 40Ca+ ion as our basis states to create out superposition state. We apply an algorithm involving carrier, red and blue sideband pulses to create out superposition states after preparing our ion in the qubit and motional ground state, |0, g>. By working backwards by beginning in the target state and moving to the ground state, we are able to work out the type and length of pulses we need to create our superposition state, with an example shown in figure 1.  

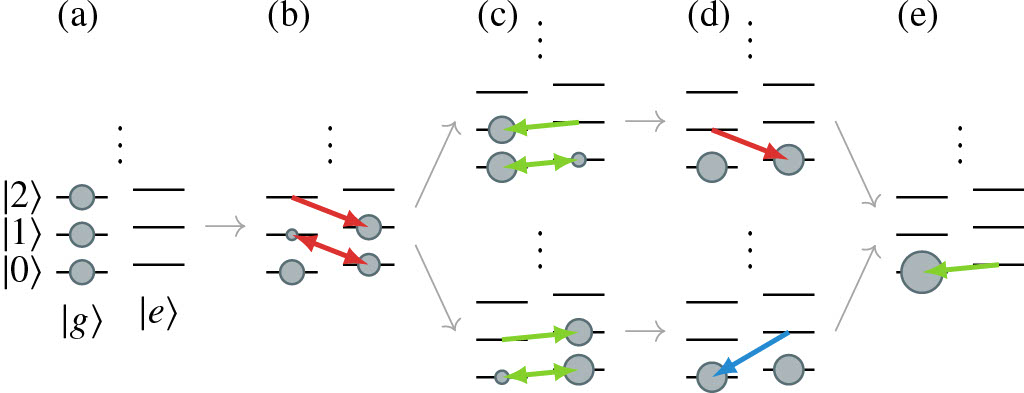
We primarily aimed to demonstrate the creation of a three element state given by,

By preparing our ion in this state, we can first observe the Rabi frequency coupling of each motional state by observing the time evolution while driving the blue sideband transition which can be seen in figure 2. The Rabi frequency coupling the |g, 0> to the |e, 1> states (a blue sideband transition) was measured to be 6.94kHz, with with each oscillation frequency for the state |g, n> increasing by a factor of √(n+1)

Evidence of oscillatory behaviour in a standard Ramsey experiment is enough to verify 2-coherence. However, a higher-order extention of the Ramsey experiment is required to verify multilevel coherence. An input state which is tested for coherence undergoes a free evolution of a controlled duration, either by waiting an amount of time or phase-shifting the control fields. Since our motional states cannot be individually probed, a measurement-mapping operation is required that maps the expected state onto the one qubit state after undergoing this free evolution. 

We implement the free-evolution of a state by changing the phase of the sideband pulses applied between the state creation and measurement-mapping sequences. Figure 3 shows the interference pattern for different superposition states, with their certified coherence values given. Plot a shows an initial demonstration of the coherence certifier with the value of 1.090 verifying two-level coherence. We were then able to demonstrate the creation of a triple state and verifying its three-level coherence in plot b, with the certifier exceeding the threhold with a value of 1.54. The final plot shows an attempt at creating a 4 state, which provides evidence that the certifier is unable to provide a false positive. 

The decoherence of our quantum system arising from multiple sources prevented the creation of the 4-state as the creation and mapping sequence began approaching the motional coherence time of our experimental set up.