Dr Kengo Deguchi: Freestream coherent structures
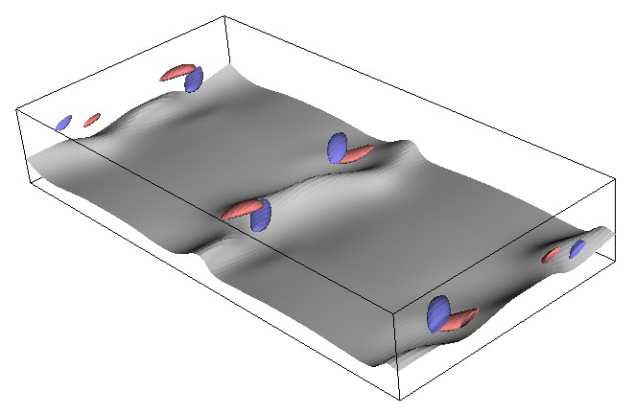 Kengo's area of interest is particular flow states embedded in laminar-turbulent transition, called "exact coherent structures” (ECS). In the most of the studies of ECS in shear-flows, the flow is assumed to be a simple wall-bounded configuration. Kengo's research aims to extend the theoretical results of ECS obtained so far to more realistic external boundary layer flows, which typically appears at an aeroplane wing.
Kengo's area of interest is particular flow states embedded in laminar-turbulent transition, called "exact coherent structures” (ECS). In the most of the studies of ECS in shear-flows, the flow is assumed to be a simple wall-bounded configuration. Kengo's research aims to extend the theoretical results of ECS obtained so far to more realistic external boundary layer flows, which typically appears at an aeroplane wing.
blah
More detail and links to research outputs
The analysis starts from an interior flow called plane Couette flow, which is a fluid flow in mutually sliding parallel plates, and then is extended to external flow. Plane Couette flow is the simplest modeling of shear flows and ECS of this problem have already been computed by Newton’s method applying to the governing equations. To make the connection between these results and external flow version of ECS study, we plan to apply many Newton's method during the gradual transformation from plane Couette flow to external flows. The behaviour of ECS helps theoretical derivation of some reduced problems valid in high Reynolds number situation. The ECS of the reduced problems are also accessible by using Newton's method.
One of Kengo's achievements is that he has extended vortex-wave interaction equations to a long-wavelength situation for plane Couette flow. It is found that the solutions of this reduced system have localized structure similar to turbulent spots frequently observed in boundary layer flow. In order to develop similar spot study in boundary-layer flow, he is now trying to solve the ECS of the full and reduced external flow problems, such as asymptotic suction boundary layer flow or Blasius boundary layer flow.
Publications
Kengo Deguchi and Philip Hall (2014). Free-stream coherent structures in parallel boundary-layer flows. Journal of Fluid Mechanics, 752, pp 602-625 doi:10.1017/jfm.2014.282
K. Deguchi, P. Hall (2014a). Canonical exact coherent structures embedded in high Reynolds number flows. Phil. Trans. R. Soc. A: 2014 372 20130352; DOI: 10.1098/rsta.2013.0352. Published 16 June 2014
Kengo Deguchi and Philip Hall (2014b). The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow . Journal of Fluid Mechanics, 750, pp 99-112 doi:10.1017/jfm.2014.234
Kengo Deguchi, Philip Hall and Andrew Walton (2013). The emergence of localized vortex–wave interaction states in plane Couette flow. Journal of Fluid Mechanics, 721, pp 58-85 doi:10.1017/jfm.2013.27
Joseph Maestri: Turbulence in channel flows
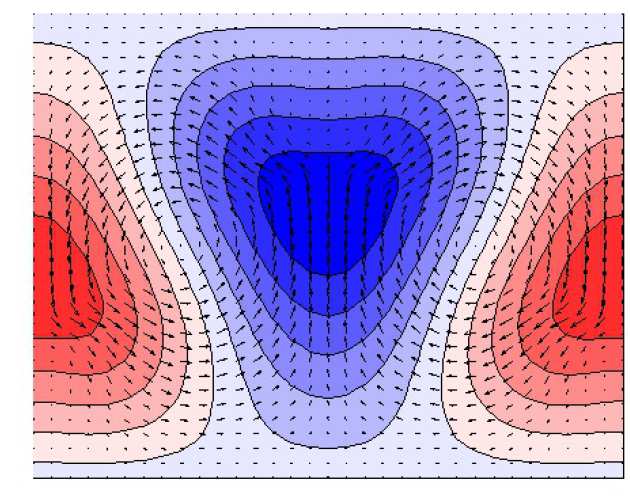 Joseph's research primarily involves the study of turbulence in channel flows. He is interested in the patterns and structures that arise during the onset of turbulence which are called “exact-coherent structures” (ECS). One aspect of Joseph's research is to investigate viable techniques, such as using periodic wall suction, to reduce the overall drag of such structures.
Joseph's research primarily involves the study of turbulence in channel flows. He is interested in the patterns and structures that arise during the onset of turbulence which are called “exact-coherent structures” (ECS). One aspect of Joseph's research is to investigate viable techniques, such as using periodic wall suction, to reduce the overall drag of such structures.
blah
More detail and links to research outputs
Exact-coherent structures have been the subject of great interest over the past couple of decades due to their relevance in understanding the process of transition to turbulence in flows without a linear instability. Over the past few years the relationship between the high Reynolds number theory of vortex-wave interaction and such structures has been elucidated in a number of papers by Hall and co-authors, see Hall and Sherwin (2010) for example.
Joseph's research involves using the asymptotic theory of vortex-wave interaction as a means of finding exact-coherent structures in shear flows. Since the asymptotic theory is a formally reduced model, our computational method is arguably faster than current methods that depend on solving the fully resolved Navier-Stokes equations.
The foundation of Joseph's work is based on the method of matched asymptotics to derive the governing vortex-wave interaction equations. Joseph's numerical work employs a number of techniques including the boundary integral method, compact finite-difference schemes and Arnoldi methods to solve large sparse eigenvalue problems.
Some key achievements of Joseph's work include:
- Development of a robust numerical scheme to solve the vortex-wave interaction equations.
- More detailed parameter study of vortex-wave interaction states in channel flows.
- Analysis of possible drag reduction techniques, including wall suction and wall waviness.
Matthew Gipon: Transition to turbulence of axisymmetric flow in cyclindrical geometry
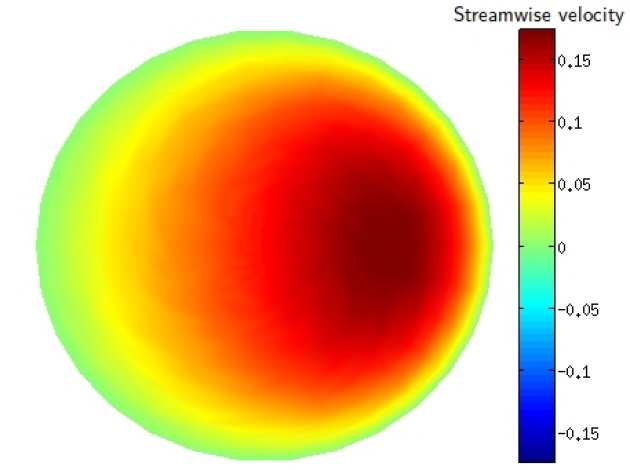 Matthew is researching transition to turbulence prediction, specifically focusing on cylindrical geometry which could be used to model flow on aircraft fuselages or inside turbine engines. For this project, numerical modelling of the three dimensional parabolic stability equations (3D PSE) will be used for the basis of the research.
Matthew is researching transition to turbulence prediction, specifically focusing on cylindrical geometry which could be used to model flow on aircraft fuselages or inside turbine engines. For this project, numerical modelling of the three dimensional parabolic stability equations (3D PSE) will be used for the basis of the research.
blah
More detail and links to research outputs
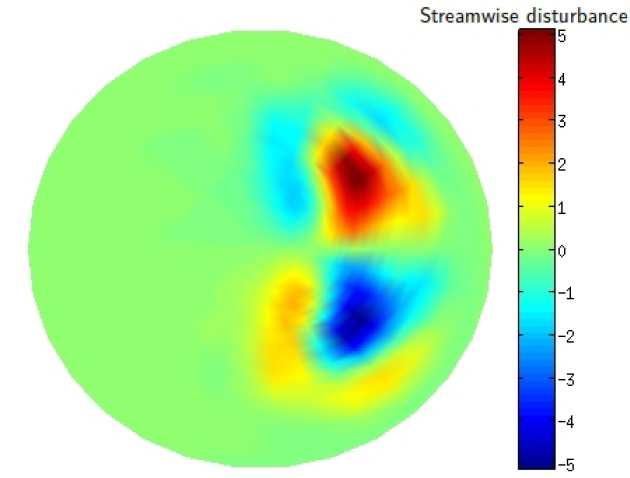 As is common the model begins with non-dimensionalised Navier-Stokes equations, which are then perturbed with three-dimensional infinitesimal disturbances. The disturbances are modelled to have wave-like nature and a slowly changing profile in the streamwise direction. To get a solution at an initial streamwise position, traditional hydrodynamic stability theory is followed and the streamwise derivatives are considered small enough to ignore. The equations of this planar problem can be reordered and solved as a generalized eigenvalue problem. In the second step the first derivatives of the disturbances in the streamwise direction are reintroduced to problem, by virtue of the perturbations being only weakly elliptic in this direction. The equations have been 'parabolized' and the results from the initial point can be marched downstream with a simple Euler method, resulting in a full picture of the three-dimensional development of the base flow and the disturbances downstream. This method is solved numerically via a Chebyshev-Fourier spectral discretisation and it has a huge computational efficiency advantage over using Direct Numerical Simulation (DNS). This approach also is much more accurate than traditional methods at high frequencies as it only requires the parallel flow assumption at the first step.
As is common the model begins with non-dimensionalised Navier-Stokes equations, which are then perturbed with three-dimensional infinitesimal disturbances. The disturbances are modelled to have wave-like nature and a slowly changing profile in the streamwise direction. To get a solution at an initial streamwise position, traditional hydrodynamic stability theory is followed and the streamwise derivatives are considered small enough to ignore. The equations of this planar problem can be reordered and solved as a generalized eigenvalue problem. In the second step the first derivatives of the disturbances in the streamwise direction are reintroduced to problem, by virtue of the perturbations being only weakly elliptic in this direction. The equations have been 'parabolized' and the results from the initial point can be marched downstream with a simple Euler method, resulting in a full picture of the three-dimensional development of the base flow and the disturbances downstream. This method is solved numerically via a Chebyshev-Fourier spectral discretisation and it has a huge computational efficiency advantage over using Direct Numerical Simulation (DNS). This approach also is much more accurate than traditional methods at high frequencies as it only requires the parallel flow assumption at the first step.
Dr Alex White: Vortex instability on walls of varying curvature
 Alex was a member of the programme until April 2014, working on external flows and the transition to turbulence, as follows:
Alex was a member of the programme until April 2014, working on external flows and the transition to turbulence, as follows:
(i) Receptivity of flows over concave surfaces;
(ii) Distributed receptivity in transonic flow;
(iii) Crossflow vortices on a swept Joukowski airfoil induced by free-stream turbulence.
blah
More detail and links to research outputs
(i) Receptivity of flows over concave surfaces
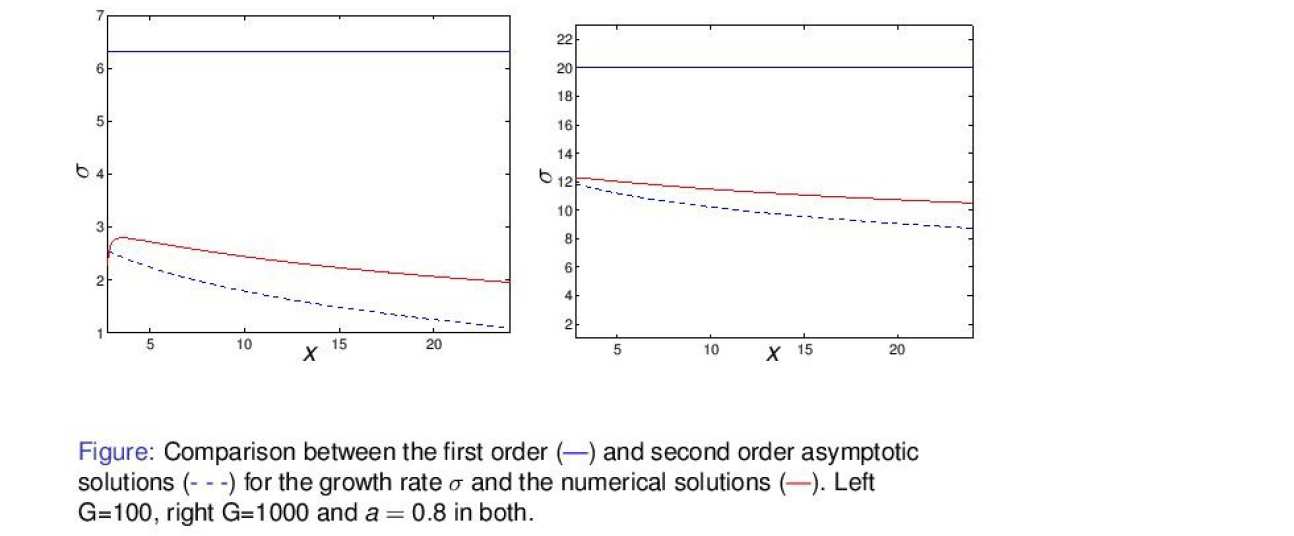
The generation of Gortler vortices is studied using both high Reynolds number asymptotic theory and numerical approaches. Of prime importance in the laminar to turbulent transition via the Gortler mechanism is the receptivity coefficient which gives the measure of the amplitude of the generated disturbance. Receptivity mechanisms of interest aresurface roughness and free-stream turbulence in the form of convected gusts. The figure on the right shows growth rates for Gortler vortices calculated with asymptotic theory at high Gortler number and numerical marching of the full parabolic system.
(ii) Distributed receptivity in transonic flow
This study aims to quantify the generation of the Tollmien-Schlichting waves using asymptotic analysis of the Navier-Stokes equations in the limit of large Reynolds number, Re at transonic speeds. The receptivity mechanism of interest belongs to the distributed receptivity class, where the Tollmien-Schlichting wave grows over a resonance region which is much wider as compared to the Tollmien-Schlichting wave length but small as compared to the wing chord. In this resonance region the effects of non-parallelism and non-linearity are of equal importance. A linear partial differential equation for the amplitude of the Tollmien-Schlichting wave generated has been derived.
(iii) Crossflow vortices on a swept Joukowski airfoil induced by free-stream turbulence
Here, convective gusts are taken as a simple model for a patch of free-stream turbulence. If the amplitude of the gust is small the linearised Euler equations come into operation, far from the surface of the airfoil. The solution of this perturbed system can be split into a rotational and irrotational velocity as described by (Goldstein 1978 JFM). This effectively leads to a mixed boundary value problem and can be solved numerically or with a Wiener-Hopf technique. The solution to this problem gives the upper boundary condition needed for the viscous boundary layer equations. These equations can then be marched downstream numerically, in order to find the relevant growth rates for the crossflow vortices, with different sweep angles and angles of attack.

