This website, while active, is no longer being frequently updated. For the most recent information visit our Oxford website: https://mechmat.web.ox.ac.uk/
Our interests span a wide range of research challenges that lie at the interface between mechanics and other disciplines, such as materials science, geology, chemistry and structural engineering. We enjoy addressing fundamental scientific conundrums that have important implications for technology development and engineering practice. Some examples of our recent research endeavours are provided in the following sections.
Hydrogen embrittlement
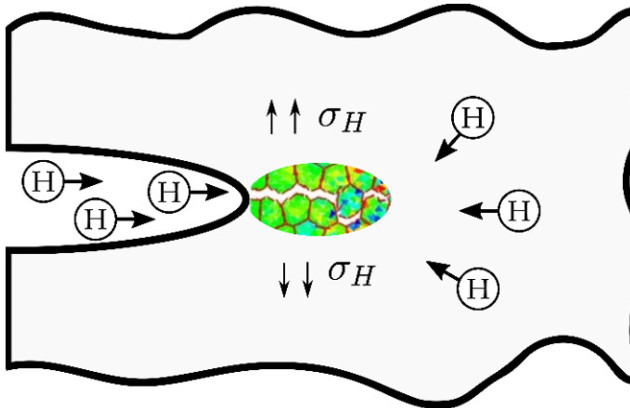 Hydrogen is famed for causing catastrophic failures in metallic components. The ductility and fracture resistance of metals are drastically reduced in the presence of hydrogen and these effects increase with material strength; a 90% reduction in fracture toughness is observed in high strength steels. However, due to the complicated multi-physics and multi-scale nature of the problem, the accurate prediction of the lifetime of engineering components undergoing hydrogen assisted fracture remains an elusive goal.
Hydrogen is famed for causing catastrophic failures in metallic components. The ductility and fracture resistance of metals are drastically reduced in the presence of hydrogen and these effects increase with material strength; a 90% reduction in fracture toughness is observed in high strength steels. However, due to the complicated multi-physics and multi-scale nature of the problem, the accurate prediction of the lifetime of engineering components undergoing hydrogen assisted fracture remains an elusive goal.
We have aimed at solving this scientific challenge by applying a mechanics rationale to identify the first-order effects governing the fracture process. Specifically, we placed our efforts in enriching continuum models to resolve the critical variables of the problem – crack tip stresses [Martínez-Pañeda & Betegón, 2015] and hydrogen concentration [Martínez-Pañeda et al., 2016] – over the critical distance at which cracking initiates, a few microns or less. Ultimately, we proposed an implicitly multi-scale model that shows an unprecedented level of agreement with experiments on various high-strength alloys and over a very wide range of applied potentials [Martínez-Pañeda et al., 2016b]. We then proceed to develop computational multi-physics models that enable fracture [Martínez-Pañeda et al., 2018] and fatigue [del Busto et al., 2017] life predictions of industrial components as a function of the material properties, the environment and the loading conditions. In addition, we have shown how early cracking puts into question the use of slow strain rate tests (SSRT) for measuring hydrogen embrittlement susceptibility [Martínez-Pañeda et al., 2020].
Crack tip plasticity: the role of dislocation hardening
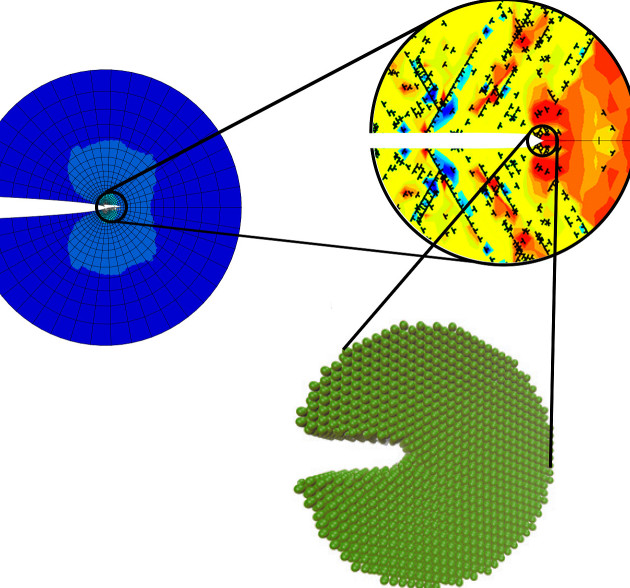 Macroscopic fracturing in metallic materials depends sensitively on properties that pertain to the micro and atomic scales. Continuum theories can be enriched to link scales in fracture mechanics and properly characterise material behaviour at the small scales involved in crack tip deformation.
Macroscopic fracturing in metallic materials depends sensitively on properties that pertain to the micro and atomic scales. Continuum theories can be enriched to link scales in fracture mechanics and properly characterise material behaviour at the small scales involved in crack tip deformation.
Of utmost importance to fracture processes that take place within microns ahead of the crack is the role of plastic strain gradients in elevating crack tip stresses. Non-homogeneous plastic deformation requires extra storage of geometrically necessary dislocations (GNDs) to accommodate lattice curvature. As shown by discrete dislocation simulations, the resulting increased dislocation density promotes local strain hardening and leads to high crack tip stresses that are much larger than those predicted by conventional plasticity. Crack tip gradient hardening can be captured at the continuum level by using strain gradient plasticity theory. We develop suitable numerical frameworks to characterise crack tip stresses under small and large strains [Martínez-Pañeda and Niordson, 2016], as well as modelling crack growth resistance [Martínez-Pañeda et al., 2019]. Moreover, our theoretical and numerical analyses reveal the existence of an elastic core at the crack tip, reminiscent of dislocation free-zones, where the stresses exhibit the linear elastic singularity [Martínez-Pañeda and Fleck, 2019; Fuentes-Alonso and Martínez-Pañeda, 2020]. We have shown that the high crack tip stresses predicted by strain gradient plasticity provide a rational basis to understand: (1) brittle fracture in the presence of plasticity (quasi-cleavage), as observed in many material systems, such as metal-ceramic interfaces or ferritic steels at low temperatures [Martínez-Pañeda et al., 2019b]; and (2) the brittle fracture of otherwise ductile steels that have been exposed to embrittlement species [Martínez-Pañeda et al., 2016].
Another interesting research question is: how much do kinematic hardening effects affect crack growth in static/monotonic fracture? Unlike fatigue analysis, isotropic hardening has been the de facto choice for modelling crack growth resistance under static loading. Contrarily, we show that kinematic/anisotropic plastic hardening effects, so far neglected, play a fundamental role under monotonic loading due to non-proportional straining as the crack advances. Our numerical results show that fracture toughness values can easily duplicate when these kinematic hardening effects are accounted for [Martínez-Pañeda and Fleck, 2018; Juul et al., 2019]. The results could have important implications for R-curve based damage assessment.
Computational fracture methods
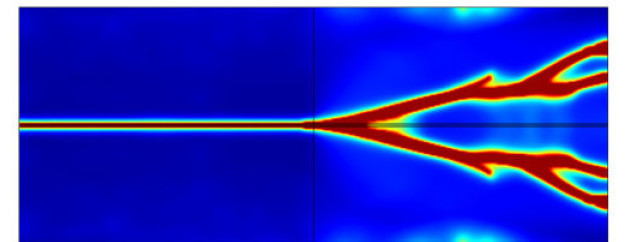 The past two decades have witnessed a dramatic growth in the development of computational tools for fracture mechanics, despite the challenges associated with modelling evolving discontinuities. Attention has shifted from the analysis of stationary cracks (computation of stress intensity factors and J-integral) to the modelling of crack growth and other complex features such as branching, merging or fragmentation. Our contributions can be classified into three fronts.
The past two decades have witnessed a dramatic growth in the development of computational tools for fracture mechanics, despite the challenges associated with modelling evolving discontinuities. Attention has shifted from the analysis of stationary cracks (computation of stress intensity factors and J-integral) to the modelling of crack growth and other complex features such as branching, merging or fragmentation. Our contributions can be classified into three fronts.
First, we have contributed to the success of cohesive zone models. On the one side, we developed new control algorithms that enable capturing crack growth using cohesive elements without convergence problems [Martínez-Pañeda et al. 2017] and eliminating the iterative procedure intrinsic to steady state analyses [Juul et al., 2019]. This has enabled us to compute R-curves and explore the influence of crack tip dislocation hardening and plastic dissipation [Martínez-Pañeda and Fleck, 2018; Martínez-Pañeda et al., 2019]. On the other side, we have developed Abaqus2Matlab [Papazafeiropoulos et al., 2017], a comprehensive piece of software that couples Abaqus and Matlab, enabling (for example) estimating the cohesive parameters by means of neural networks.
Second, we have contributed to the development of the eXtended Finite Element Method (X-FEM) by presenting a new X-FEM non-linear framework for elastic-plastic solids [Martínez-Pañeda et al., 2017]. The scheme is capable of capturing the stress elevation due to strain gradients by means of suitably defined asymptotic functions. In addition, it includes (i) higher order elements, (ii) a linear weighting function for the blending elements, (iii) an iterative solver for nonlinear systems and (iv) an appropriate triangular integration scheme.
Third, we have embraced the remarkable success of the phase field fracture method with relish. The phase field fracture method is a very robust tool, with sound underlying physics (based on the concepts of fracture energy and a process zone) and capable of capturing complex crack phenomena, such as crack nucleation at arbitrary sites, crack growth along complex trajectories, and branching and coalescence of multiple cracks. Our contributions lie in the development of (1) a phase field formulation for functionally graded materials [Hirshikesh et al., 2019], (2) a multi-physics deformation-diffusion-fracture framework, particularised to the case of hydrogen embrittlement [Martínez-Pañeda et al., 2018], and (3) quasi-Newton monolithic solution schemes, that reveal notable computational gains [Kristensen and Martínez-Pañeda, 2020].
Small Scale Testing Methodologies
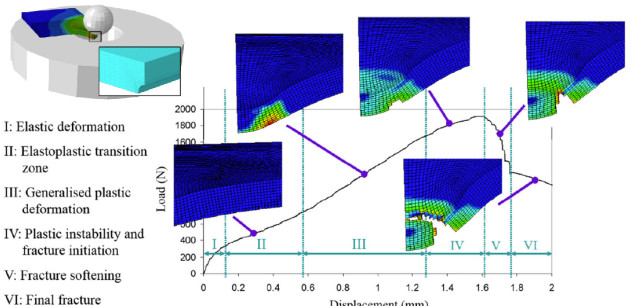 Miniature testing devices and techniques are gaining increasing traction due to their capabilities in performing material assessment in an (almost) non-destructive manner. Among the different experimental techniques proposed, the Small Punch Test is particularly popular, as it has proven capable of reliably characterising the mechanical response when little material is available – i.e., heat-affected zones, irradiated material, etc.
Miniature testing devices and techniques are gaining increasing traction due to their capabilities in performing material assessment in an (almost) non-destructive manner. Among the different experimental techniques proposed, the Small Punch Test is particularly popular, as it has proven capable of reliably characterising the mechanical response when little material is available – i.e., heat-affected zones, irradiated material, etc.
We have aimed at extending the success of the Small Punch Test to the assessment of fracture properties by introducing different notched geometries, to accommodate different triaxiality conditions [Cuesta et al., 2019]. We have also presented new hybrid experimental-numerical methodologies based on the crack tip opening displacement [Martínez-Pañeda et al., 2016]. Understanding damage initiation and subsequent failure required conducting Gurson-type analyses of material failure [Martínez-Pañeda et al., 2016b]. And, more recently, we have employed the Small Punch Test to characterise additively manufactured metallic [Cuesta et al., 2019] and polymer samples [Cuesta et al., 2019]. These research achievements are being exploited commercially by the spin-off company KHIS group.
Mechanics of Functionally Graded Materials
 There is an emerging interest in the analysis of the mechanical response of materials with spatially varying properties. New manufacturing technologies make it possible to engineer materials with functionally graded microstructures, so-called functionally graded materials (FGMs). The resulting spatial variation of material properties eliminates stress discontinuities at material interfaces and optimises material performance under non-uniform service conditions. For example, the performance of coatings subjected to large thermal gradients can be significantly improved by using metal-ceramic FGMs, which combine the thermal and corrosive resistance of ceramics with the mechanical strength and high tenacity of metals.
There is an emerging interest in the analysis of the mechanical response of materials with spatially varying properties. New manufacturing technologies make it possible to engineer materials with functionally graded microstructures, so-called functionally graded materials (FGMs). The resulting spatial variation of material properties eliminates stress discontinuities at material interfaces and optimises material performance under non-uniform service conditions. For example, the performance of coatings subjected to large thermal gradients can be significantly improved by using metal-ceramic FGMs, which combine the thermal and corrosive resistance of ceramics with the mechanical strength and high tenacity of metals.
We aim at facilitating this technological disruption by presenting suitable numerical schemes to introduce the gradient in both elastic [Martínez-Pañeda, 2019] and elastic-plastic [Mathew et al., 2019] properties into a finite element framework. In addition, we have devoted efforts to model and understand the fracture of FGMs, which often constitutes the primary design criterion. The challenge lies in capturing the complex crack trajectories that arise as a consequence of the crack tip mode mixity induced by the spatial variation of material properties. We have presented new numerical solutions in the context of the X-FEM [Martínez-Pañeda and Gallego, 2015] and phase field fracture [Hirshikesh et al. 2019] methods that show a very satisfactory agreement with experimental observations.
Contact us
Write to e.martinez-paneda@imperial.ac.uk for establishing a collaboration or to inquire for vacancies.