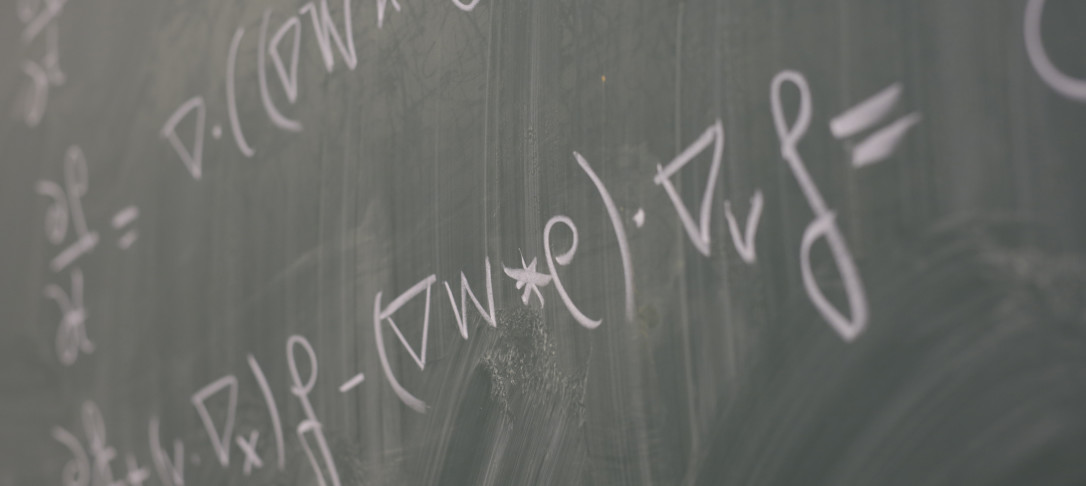
Title
Nonradial stability of self-similarly expanding Goldreich-Weber stars
Abstract
A fundamental model of a self-gravitating star is given by the Euler-Poisson equation in the setting of a free boundary problem. At the mass critical index, there exists a known class of spherically symmetric (self-similarly) expanding solutions, called the Goldreich-Weber solutions, modelling expanding stars. We establish non-radial non-linear stability of this class of solutions, extending existing results on radial stability. In doing so, we proved global-in-time existence for a larger class of expanding solutions around the known class that’s not spherically symmetric but behaves similarly.
More precisely, we prove that any given self-similarly expanding Goldreich-Weber star is codimension-4 stable in the class of irrotational perturbations. The codimension-4 condition is optimal and reflects the presence of 4 unstable directions of the linearised operator in self-similar coordinates, which are induced by the conservation of the energy and the momentum. This result can be viewed as the codimension-1 nonlinear stability of the “manifold” of self-similarly expanding GW-stars in the class of irrotational perturbations.
Please note that the seminar will take place in person in room 140 of Huxley Building.