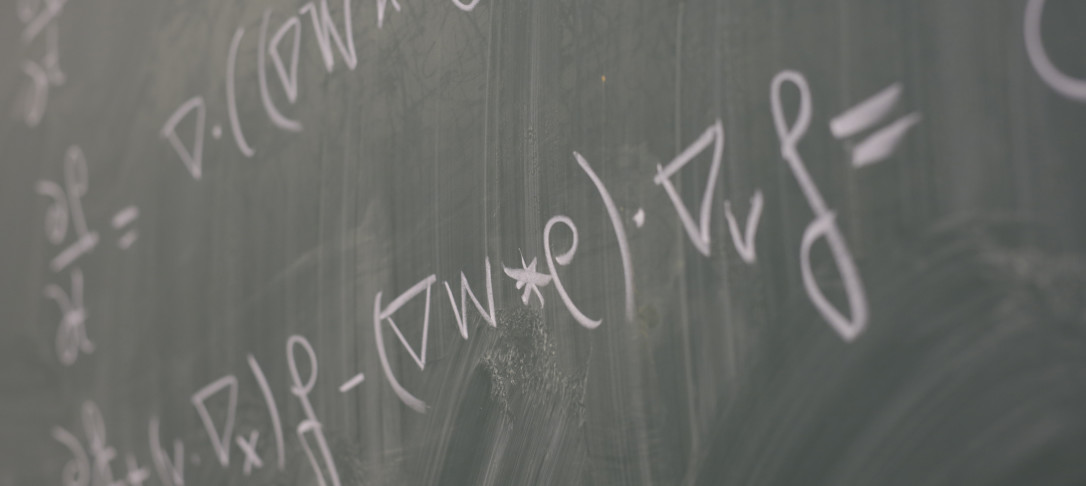
Title
Self-repelling Brownian polymer in the critical dimension
Abstract
The Self-Repelling Brownian Polymer is a type of weakly self-avoiding motion in R^d that was introduced separately by physicists (Amit, Parisi, Peliti, ’83) and probabilists (Norris, Rogers, Williams, ’87). In dimension d = 3 and higher, the process converges to Brownian motion under a diffusive rescaling, whereas, in the critical dimension, d = 2, the process is logarithmically super-diffusive. Nonetheless, we can show that in the limit we still recover Brownian motion, provided that the rescaling is done in the “weak coupling” sense, whereby as we zoom out, we also tune down the strength of self-interaction. In this talk, I will define the model and discuss the recent techniques that give this result. This is a work in progress with Giuseppe Cannizzaro.
Please note that the seminar will take place in person in room 642 of Huxley Building.