Evangelia Skiada

Consistent Incorporation of Topography Effects in Ground Motion Prediction Models

Started: October 2013
Supervisor: Kontoe, S.; Stafford, P.
Funding: Departmental award

Background

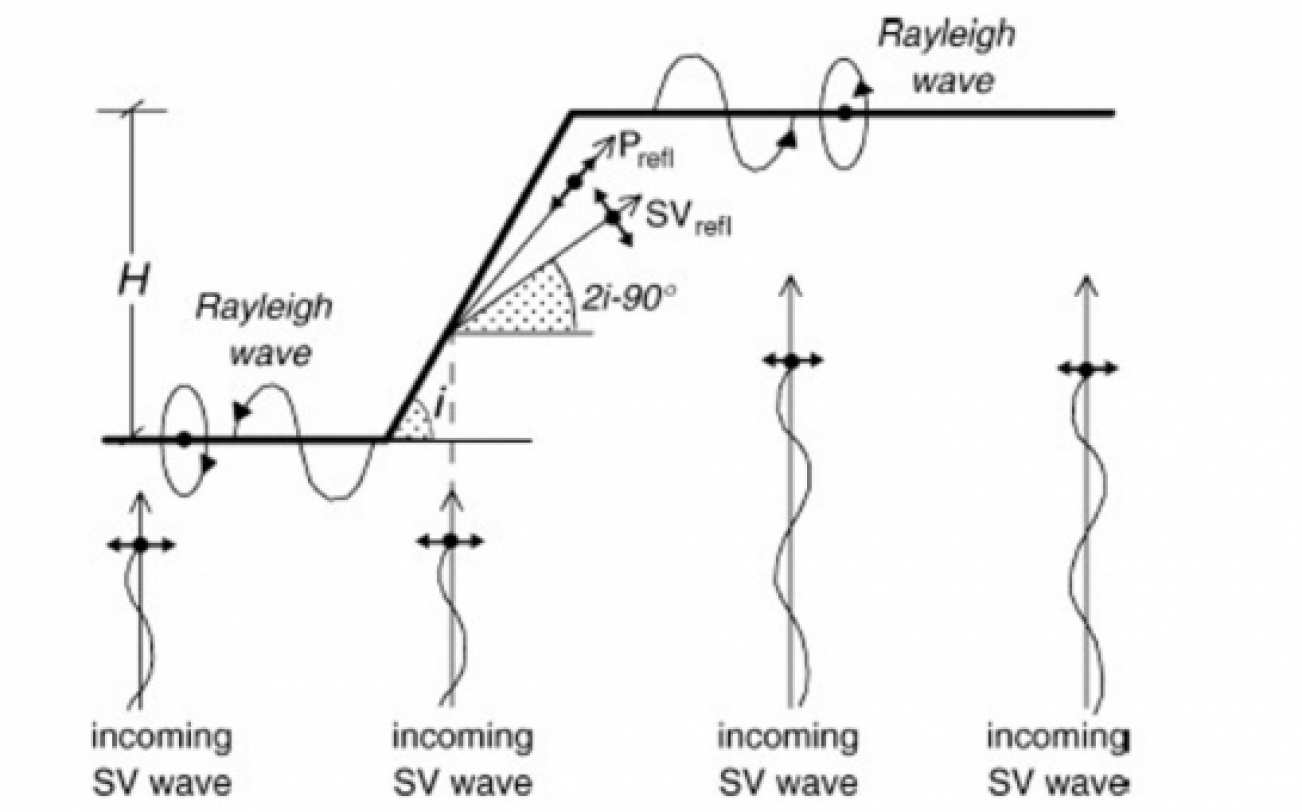
Topographic amplification of seismic motions has been well recognized even before any instrumental records of ground motions were available. Documented observations from destructive earthquakes have shown that damaging effects tend to increase where steep relief of complicated topography is present (Figure 1). In the recent past, there have been numerous cases of recorded motions (e.g. Northridge (1994), Athens (1999), Haiti (2010) and Christchurch (2011)) and field experiments that provide evidence of topographical effects on seismic motion. The magnitude of topography induced amplification can be significant, typically 2-3 times the free-field motion (Pedersen et al 1994), but amplifications up to 30 times have also been reported in the literature (Geli et al 1988). Due to the limited number of instrumented evidence from major earthquakes and the quantitative disagreement between theory and observations, nowadays topographic amplification phenomena are still not very well understood. Unlike amplification due to soil layering, there is very little guidance available in most seismic code provisions for topographic effects despite their significance in engineering practice.

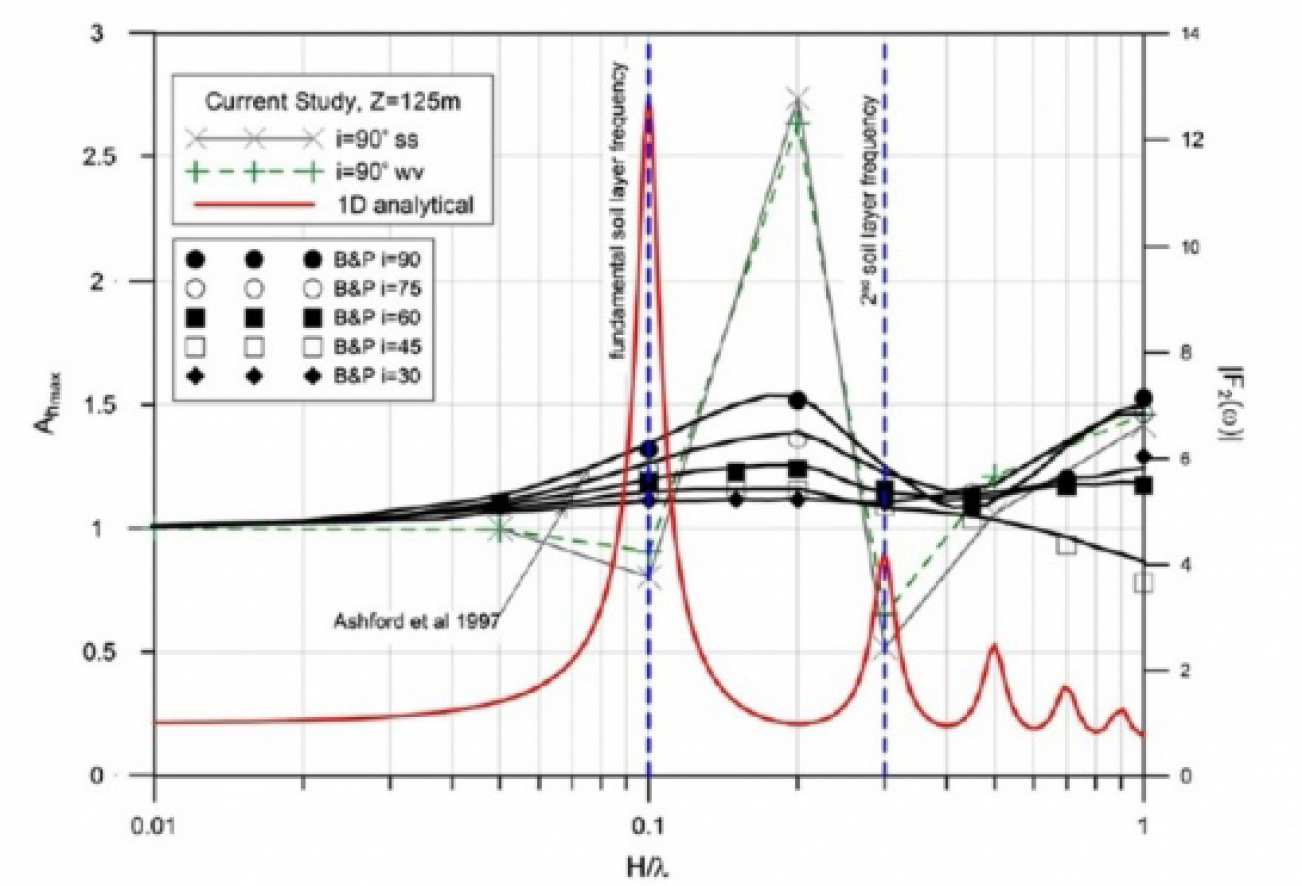
Recent work by Tripe et al (2013) at Imperial College demonstrated the interaction of topography amplification with site response (Figure 2). It was found that soil layer and topographic effects interact with the greatest interaction happening over the range of the soil layer’s natural frequencies. The topographic and soil layer amplification contributions are not easily separated with the peak amplification values occurring at different normalized frequencies of the input motion.  

Topography effects are currently incorporated in ground motion prediction equations in a very crude manner only as part of the general variability introduced by travel path and site effects. Predictive equations and design codes are associated with a greater uncertainty or a larger standard deviation and may underestimate the intensity of the actual ground shaking beneath structures located on hills and ridges. Clearly there is a need for systematic study of these effects to improve the existing code provisions and predictive tools. 

Research Aim

The research project will employ the in-house Finite Element code ICFEP (Potts & Zdravkovic, 1999) of the Geotechnics group at Imperial College to simulate the factors that contribute to the topographic amplification at a sloping ground. The code is equipped with state-of-the-art time integration schemes (Kontoe et al., 2008) and advanced boundary conditions for dynamic analysis (Kontoe et al., 2009).

Fig 1
Fig 1: Schematic illustration of incoming SV waves and induced reflected P wave, reflected SV wave and Rayleigh wave in the case of step-like slopes (i≥45o) (from Bouckovalas and Papadimitriou, 2005).

The main aspects of this PhD thesis will concern the following:

(i)   quantification of the parameters that from literature have been reported to affect topographic amplification. Parameters related to the input motion characteristics (type and direction of incident waves, frequency content of the incident motion, duration and type of the time history excitations), slope inclination, soil layering and properties are going to be examined. Actual seismic records and soil profiles will be modelled in contradiction to the majority of the reviewed studies which consider a homogeneous half-space with harmonic motion excitations;

(ii)   further parametric analyses considering only the parameters that were found to have a considerable effect to topographic amplification; and

(iii)   probabilistic consideration of the numerical modelling outputs for developing ground motion prediction equations (GMPEs) for the topographic amplification assessment. Based on the finite element results, the topographic effect of each of the examined parameters will be reviewed and additional terms in the GMPEs accounting for the topographic effects will be developed.

Fig 2
Fig 2: Topographic amplification at the slope crest and amplification function for z=125m (from Tripe et al., 2013). The results of Bouckovalas and Papadimitriou (referred to as B&P) and Ashford et al. (1997) for slopes in a homogeneous half-space are also shown (“wv” stands for wavelet and “ss” for steady state).

References
  • Ashford S., Sitar N., Lysmer J. and Deng N. (1997). Topographic effects on the seismic response of steep slopes. Bulletin of the Seismological Society of America, 87 (3), pp.701-709.
  • Bard P. and Riepl-Thomas J. (2000). Wav propagation in complex geological structures and their effect on strong ground motion. In: Kausel E. and Manolis G.D. (eds.) Wave Motion in Earthquake Engineering. Southampton, WIT Press. pp.37-95.
  • Bielak J., Loukakis K., Hisada Y. and Yoshimura C. (2003). Domain reduction method for three-dimensional earthquake modelling in localized regions. Part I: Theory. Bulletin of the Seismological Society of America, 93 (2), pp.817-824.
  • Bouckovalas G.D. and Papadimitriou A.G. (2005). Numerical evaluation of slope topography effects on seismic ground motion. Soil Dynamics and Earthquake Engineering, 25, pp.547-558.
  • Gazetas G., Kallou P.V. and Psarropoulos P.N. (2002). Topography and soil effects in the Ms 5.9 Parnitha (Athens) earthquake: the case of Adames. Natural Hazards, 27, pp.133-169.
  • Geli L., Bard P-Y and Jullien B (1988). The effect of topography on earthquake ground motion: a review and new results. Bulletin of the Seismological Society of America, 78 (1), pp.42-63. 
  • Kontoe S., Zdravkovic L. and Potts D. (2008). An assessment of the domain reduction method as an advanced boundary condition and some pitfalls in the use of conventional absorbing boundaries. International Journal for Numerical and Analytical Methods in Geomechanics, 33, pp.309-330.
  • Pedersen H., Le Brun B., Hatfield D., Campillo M. and Bard P-Y (1994). Ground motion amplitude across ridges. Bulletin of the Seismological Society of America, 84 (6), pp.1786-1800. 
  • Potts, D.M. & Zdravkovic, L. (1999) Finite Element Analysis in Geotechnical Engineering: Theory. London, Thomas Telford Publishing.
  • Potts, D.M. & Zdravkovic, L. (1999) Finite Element Analysis in Geotechnical Engineering: Application. London, Thomas Telford Publishing.
  • Trifunac M.D. (1971). Surface motion of a semi-cylindrical alluvial valley for incident plane SH waves. Bulletin of the Seismological Society of America, 61 (6), pp.1755-1770.
  • Tripe R., Kontoe S. and Wong T.K.C. (2013). Slope topography effects on ground motion in the presence of deep soil layers. Soil Dynamics and Earthquake Engineering, 50, pp.72-84.
  • Wong H.L. and Trifunac M.D. (1974). Surface motion of a semi-elliptical alluvial valley for incident plane SH waves. Bulletin of the Seismological Society of America, 64 (5), pp.1389-1408.

EVANGELINA SKIADA

Evangelina SkiadaPhD Candidate - Geotechnics 
Department of Civil & Environmental Engineering 
Imperial College London SW7 2AZ
evangelia.skiada11@imperial.ac.uk