Dark matter is the name given to 84% of the material in the universe whose nature is unknown but which could be composed of unidentified particles. Dark matter represents a huge gap in our understanding of the building blocks of the universe, but with enough ingenuity we can construct experiments to detect what dark matter might be.

Although we think that dark matter surrounds us, it barely interacts with ordinary matter. To see any effects from dark matter, we need an exceedingly well controlled system that we can measure very precisely. A particle held by static electric and magnetic fields, an arrangement called a Penning trap, is perfect for this application.

 The Quantum Enhanced Particle Astrophysics  (QuEPA) project is a new effort to use   Penning trapped electrons and resonant cavity antennas to detect dark matter.

Our project is most focused on detecting a certain type of dark matter particle,  the axion. This particle can convert into a microwave photon in a strong magnetic field [1]. The rate of axion-to-photon conversion can be enhanced using a resonant cavity, in our case a Fabry-Perot made from two highly reflective mirrors. A Penning trapped electron can then be used as a single photon counter [2] to detect the microwave photons from axion decays.  Electrons in Penning traps can also be used to look for other dark matter particles such as millicharged particles, which could collide with a trapped particle and cause it to change its quantum state in a way which can be detected experimentally [3, 4]. 

We hope to use our ability to precisely control the smallest particles to shed some light onto the mysteries of dark matter.

Please read on for a technical introduction to our project.  

The axion is a hypothetical new type of particle and the first to be named after a laundry detergent. It was so-named because it “cleans up” the mystery of why the neutron’s electric dipole moment is at least around one billion times smaller than might be expected, or equivalently, why the Strong Force respects CP symmetry. It’s predicted to be an uncharged, and measurements constrain its mass to at least one million times lighter than the electron, with very weak couplings to known particles.

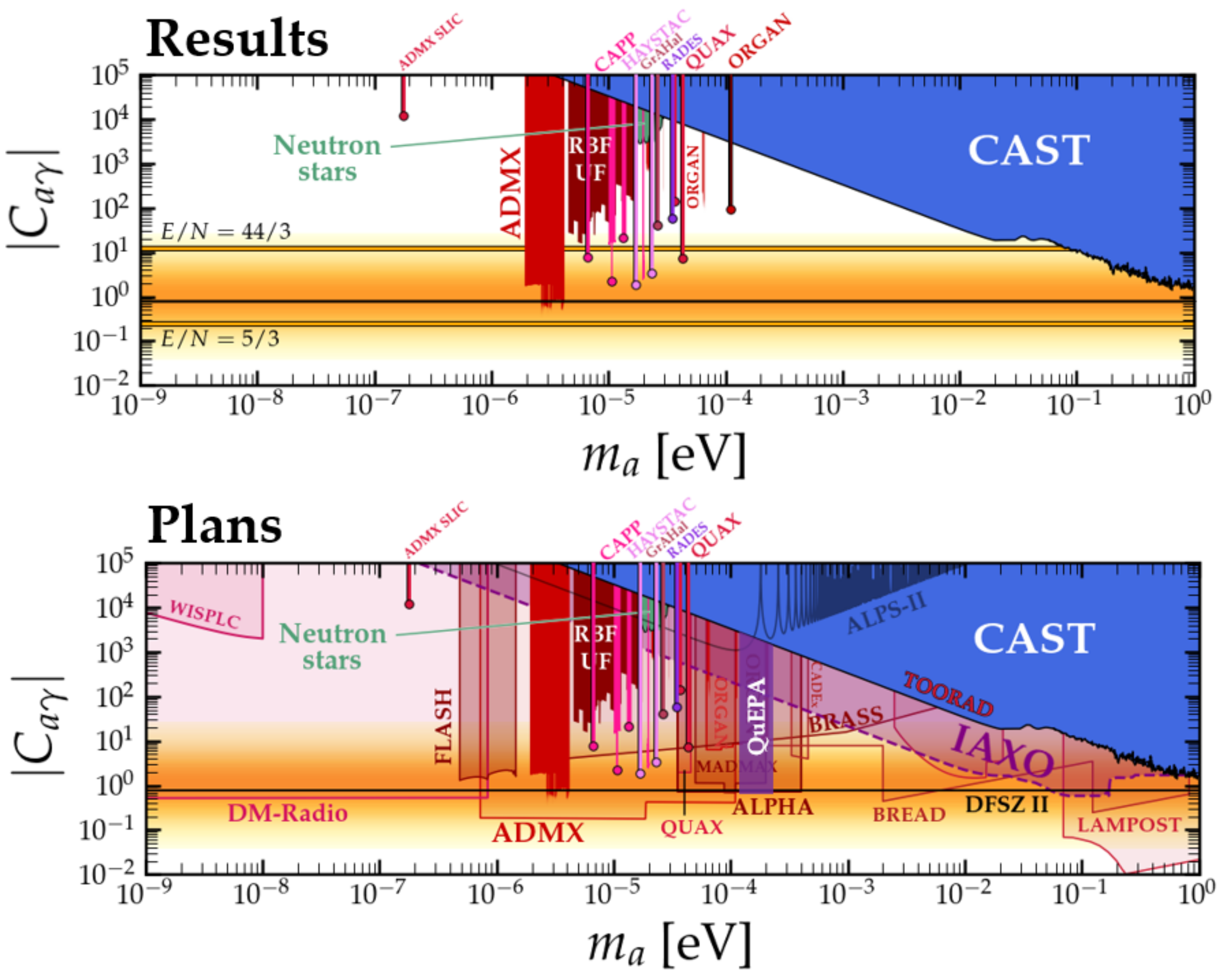
Although axions weren’t proposed with dark matter in mind, it quickly became apparent that they could well be this unknown substance. If axions existed, there were mechanisms that would lead to their production in the early universe, creating the dark matter halos we observe today. Although it is not possible to definitely predict the mass of the axion, many models suggest a possible mass between 1 and 1000 µeV. QuEPA’s short term goal is to investigate axion masses between 120-240 µeV, while developing technologies that can be used over a broader mass range 40-1000 µeV.

The top plot in shows a ploot of the constraints on the coupling between photons and axions for different axion masses m_a. The coupling is given in terms of a coupling coefficient C_Aγ which should be around 1 in most axion models. The bottom plot includes the targets of various experimental efforts, including QuEPA between 120-240 ueV. 

In a strong magnetic field, axions with mass  can convert into photons with a frequency ν_a=m_ac²/h. A haloscope attempts to detect the dark matter halo using this conversion [1]. A resonant cavity can, under the right circumstances, enhance the conversion of axions in to photons. The rate at which photons can be extracted from a cavity whose resonant frequency matches is given by:

R_out = K C_aγ² B² V_m Q .

Where K = 1 x 10^-3 HzT^-2m^-2 if axions make up all dark matter, C_aγ is a model dependent parameter around 1, Q is the cavity Q-factor and

V_m = |∫dV B·E_m|² /( ∫dV |B|² ∫dV ε_r|E_m|²) ,

is a volume representing the overlap between the electric field of the cavity mode E_m with relative permetivity ε_r and the applied magnetic field B.

So far, only the ADMX experiment operating between 2-4 ueV has reached the required senstivity to probe the DFSZ axion model, in this case using a large resonant cylindrical cavity. Scaling this approach up to higher frequncies poses a challenge. For a normal closed cavity the volume term, V_m, is basically proportional to the axion wavelength cubed, V_m ∝λ_a³∝ν_a^-3, so going from 4 µeV to 120 µeV reduces the emission rate by a factor of ~900, making it very hard to detect this weak signal in a reasonable time.

To counteract this many collaborations have suggested new concepts like plasma haloscopes [7], magnetized mirrors [8-9], magnetized mirrors with dielectric boosters [10] and dielectric haloscopes [11]. QuEPA’s approach is a Fabry-Perot cavity operating in the TEM₀₀₁ mode. This parallels the approach of the ORPHEUS collaboration, which will use TEM_00q, q~18  with dielectric inserts to achieve a large V_m [12].

Unlike a cylindrical cavity, for a Fabry-Perot V_m ∝λ_a∝ν_a^-1 so long as the mirror radius of curvature is increased for higher axion masses. It also possible to make very highly reflective mirrors which produces high quality factor cavities.

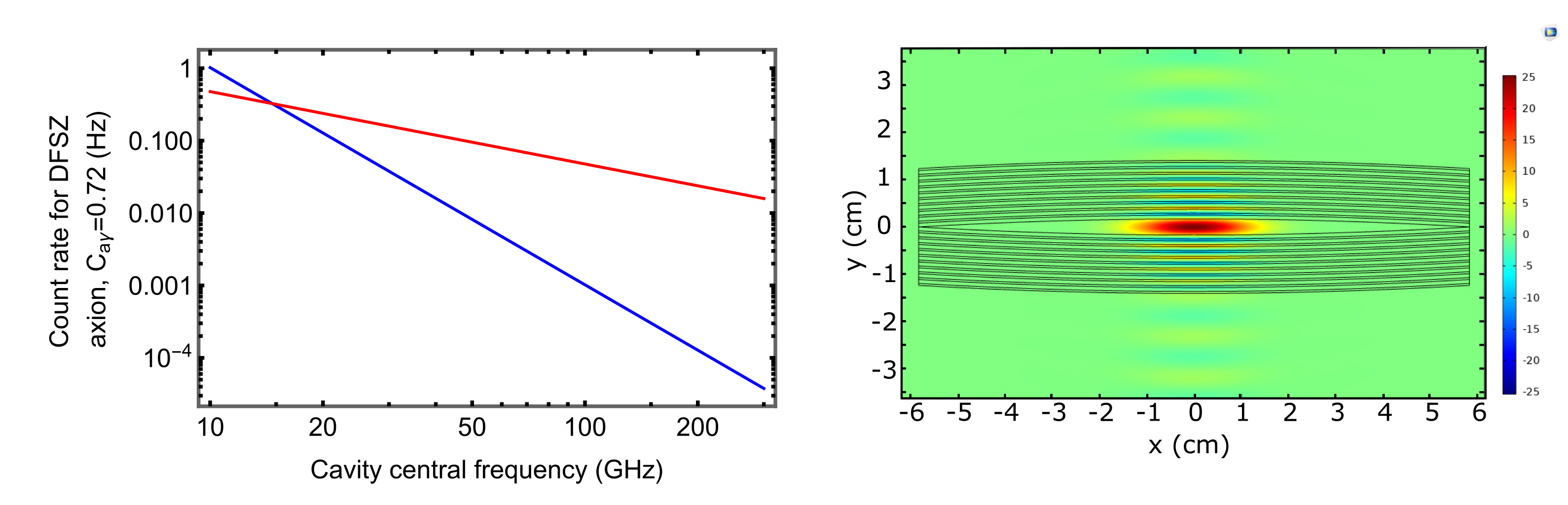
On the left hand side of Figure 3 you can see the expected R_out for a cylindrical cavity, scaled from the dimensions of the ADMX Sidecar experiment [13], and a 15 cm diameter Fabry-Perot, for a DFSZ axion (C_aγ = 0.72), in both cases using Q = 10⁶ and B = 7 T. The count rates for the Fabry-Perot outstrip the cylindrical cavity, are high enough to allow a search experiment to be conducted in a reasonable length of time.

Making a very high-Q Fabry-Perot comes with its own challenges, and we are investigating a variety of technologies including thin superconducting films, high temperature superconductors and Bragg reflectors to manufacture the mirrors. On the right hand side of the figure you can see a COMSOL simulation of the electric field inside a Fabry-Perot cavity made with Bragg mirrors.

If any axions are converted into microwave photons, these will be coupled out of the cavity and detected. At these high frequencies, it is preferable to count individual microwave photons rather than linearly amplify the microwave field using a classical amplifier, as this avoids the Standard Quantum Noise limit (SQL) [14]. A major goal of QuEPA is to develop an electron in a Penning trap as a single photon counter, plugging a region in which no technologies currently exist.

A Penning trap is a superposition of a static, homogenous magnetic field and a quadrupolar potential (see here for more information) . For an electron in magnetic fields 1-2.1 T, the modified cyclotron mode has a frequency of 30-60 GHz.

To detect single photons [2], the electron’s modified cyclotron motion will be matched to the expected frequency of the axion’s by adjusting the magnetic field. The incoming photons will change the cyclotron quantum state of the particle. This will in turn shift the axial frequency using a magnetic bottle, the same principle as used to measure the electron’s g-factor [15].

The count rates will be typically quite low (1 per 10-100 seconds), however this is perfect for an electron that has much lower thermal transition rates at 100 mK.

Electrons in Penning traps are potentially sensitive to a whole range of other dark mater particles, not just the axion. For instance, in much the same way as photons from axion conversions can change the cyclotron quantum state of the particle, collisions with fractionally charged dark matter can change the magnetron or cyclotron state of the particle [3,4]. By observing the particle for a long time and looking for these types of “quantum jumps”, it is possible to conclude whether or not unexpected particle collisions have occurred. Trapped ions already set very good limits on millicharged particles [3], and electrons have the potential to investigate potential millicharged particles in a region of interest to astrophysicists, who are seeking to explain the cooling of hydrogen around the cosmic dawn. Other authors have also demonstrated how Penning trapped electrons can be used to search for dark photons [5]. In this case the dark photon can convert into an ordinary photon at the walls of the trap, again leading to unexpected transitions in the cyclotron mode.

QuEPA is supported by the Royal Society, grant numbers URF\R1\211059 and RF\ERE\210085 and the Science and Technology Facilities Council (STFC), grant number ST/W006650/1 “A Quantum Jump Sensor for Dark Matter Detection”

[1] Sikivie P., Detection rates for ‘‘invisible’’-axion searches Phys. Rev. D 32, 2988 (1985)

[2] Cridland, A. et al., Single Microwave Photon Detection with a Trapped Electron Photonics, 3(4), 59 (2016)

[3] Budker D. et al., Millicharged dark matter detection with ion traps, PRX Quantum 3 010330  (2022)

[4] Carney D., Trapped Electrons and Ions as Particle Detectors, Phys. Rev. Lett. 127, 061804 (2021)

[5] arXiv:2208.06519 [hep-ex]

[6] C. Bartram et al., Search for "Invisible" Axion Dark Matter in the 3.3-4.2 μeV Mass Range, Phys. Rev. Lett. 127, 261803 (2021)

[7] arXiv:2210.00017 [hep-ph]

[8] http://wwwiexp.desy.de/groups/astroparticle/brass/brassweb.htm

[9] BREAD Collaboration, Broadband Solenoidal Haloscope for Terahertz Axion Detection, Phys. Rev. Lett. 128, 131801 (2022)

[10] arXiv:1901.07401v2

[11] Quiskamp et al., Sci. Adv. 8, eabq3765 (2022)

[12] R. Cervantes, G et al., ADMX-Orpheus first search for 70  μeV dark photon dark matter: Detailed design, operations, and analysis Phys. Rev. D 106, 102002 (2022)

[13] C. Boutan et al. (ADMX Collaboration), Piezoelectrically Tuned Multimode Cavity Search for Axion Dark Matter, Phys. Rev. Lett. 121, 261302  (2018)

[14] S. K. Lamoreaux, K. A. van Bibber, K. W. Lehnert, and G. Carosi, Analysis of single-photon and linear amplifier detectors for microwave cavity dark matter axion searches, Phys. Rev. D 88, 035020 (2013)

[15] S. Peil and G. Gabrielse, Observing the Quantum Limit of an Electron Cyclotron: QND Measurements of Quantum Jumps between Fock States, Phys. Rev. Lett. 83, 1287 – (1999)