AAA2w
The video above shows a simulation of the temperature of a solid target as it is heated by an intense short-pulse laser and converted to plasma. The laser enters from the left hand side and generates a flux of relativistic electrons which stream through the target and heat it to temperatures around 10 million degrees C.
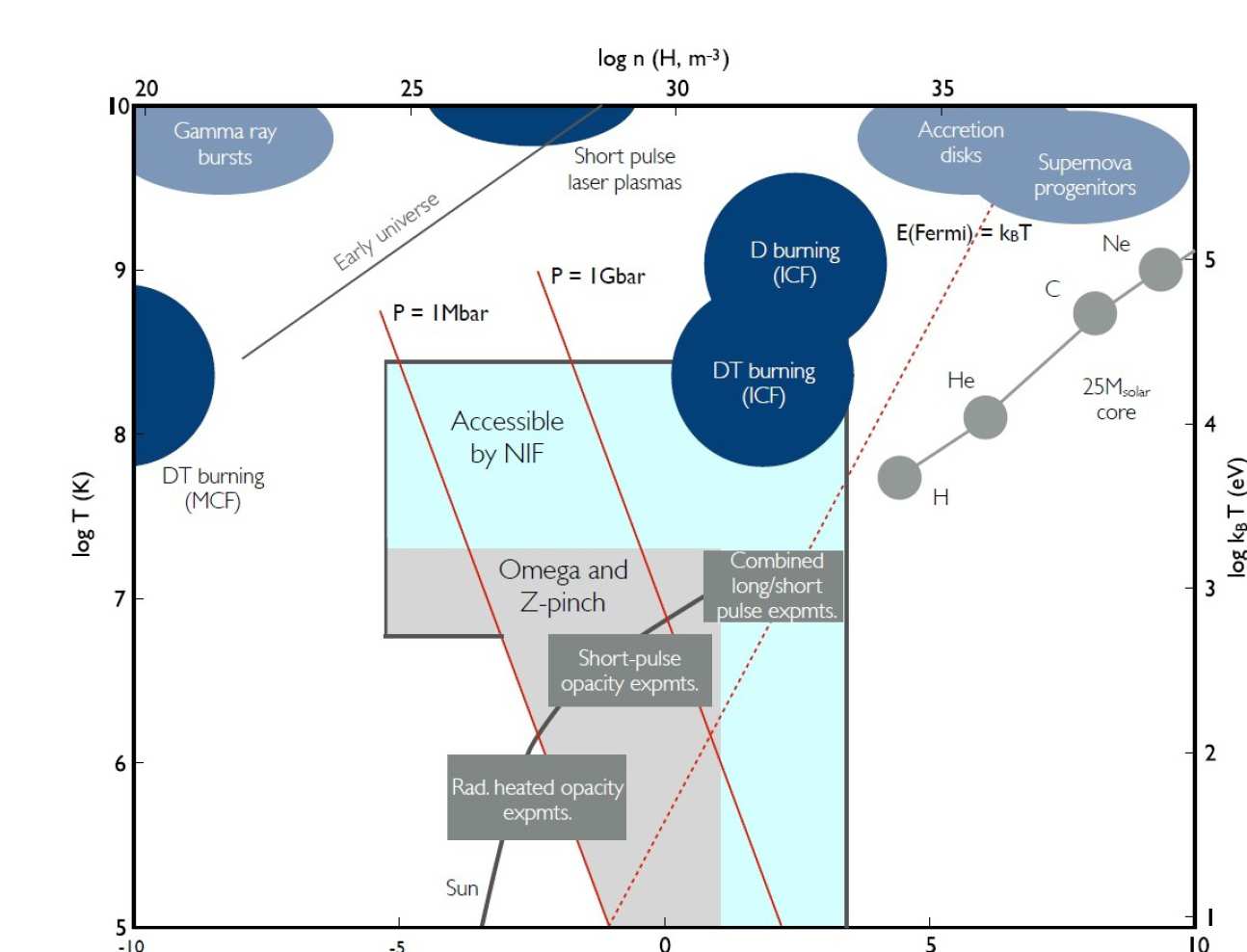 High energy density physics (HEDP) covers the interactions of matter with temperatures in excess of a million degrees C°, or densities from that of liquid water (1 gram per cubic centimetre) to many times the density of solid lead. A more technical definition is any volume with an equivalent energy density of 1011 J/m3 or more, or a pressure of 1 Mbar, or 1 million times Earth’s atmospheric pressure, and above.
High energy density physics (HEDP) covers the interactions of matter with temperatures in excess of a million degrees C°, or densities from that of liquid water (1 gram per cubic centimetre) to many times the density of solid lead. A more technical definition is any volume with an equivalent energy density of 1011 J/m3 or more, or a pressure of 1 Mbar, or 1 million times Earth’s atmospheric pressure, and above.
At these densities and energies, matter becomes plasma, also known as the fourth state of matter (the other three being solids, liquids, and gases). Plasmas are very different to the other states of matter, and support an extremely rich variety of complex physical phenomena, which makes them compelling to study. HEDP plasmas include fusion plasmas, high intensity lasers, stellar interiors, early universe plasmas, and supernovae.
High energy density physics is the focus of a small team of theorists within the Plasma Physics group at Imperial College. It includes S. J. Rose, D. Burridge and J. Beesley. Many other members of the plasma physics group also work on HEDP.
Examples of our particular research interests are listed in more detail below. We work on some of the most challenging problems in HEDP including multi-species plasmas, self-consistent emission, absorption, and scattering of radiation, non-equilibrium plasmas, the physics of inertial confinement fusion and investigations of fundamental quantum electrodynamic (QED) processes.
High Energy Density Physics
Solid density laser-plasma interactions
M. Sherlock, E. Hill, S. J. Rose
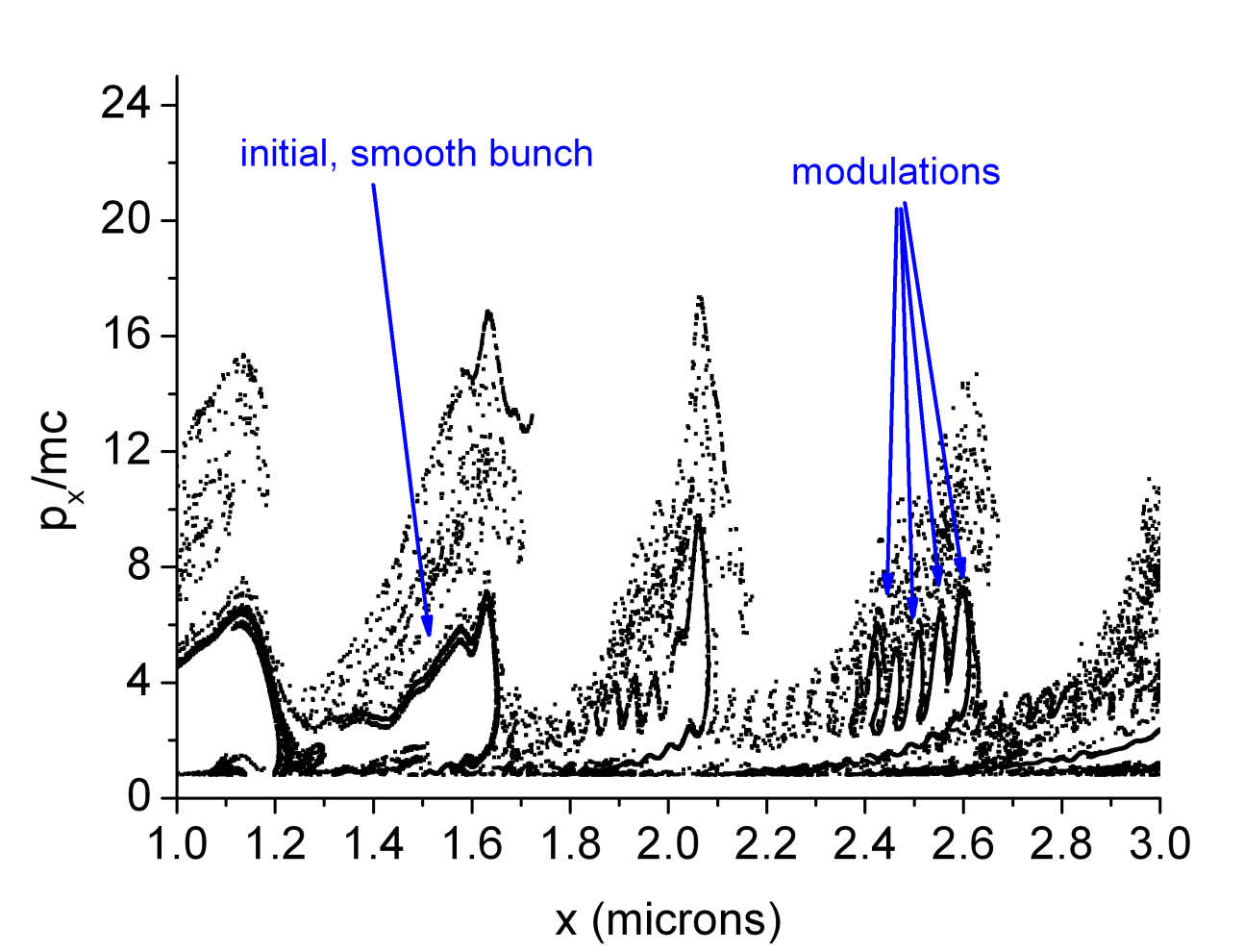 We are interested in kinetic effects in high energy density plasmas relevant to intense laser-plasma interactions and inertial confinement fusion schemes. In a plasma, there may be deviations away from equilibrium on small length or time scales, or if the particles involved are very energetic. For example, the energy transferred to a plasma by ultra intense lasers is enough to generate large fluxes of relativistic electrons which stream through the plasma and set up complex electromagnetic fields. The electron motion can be strongly affected by these fields, but short-range "collisions" between particles are also important. How to correctly model these effects and use them in existing models is a challenging computational problem because of the disparate time and length scales involved and the need to correctly couple physics from multiple disciplines. We have developed a number of codes that employ direct Fokker-Planck, expansion. and particle methods in multiple dimensions to study these effects in both electrons and ions. Due to the heavy computational cost of these simulations, we write code to run on new accelerator hardware and traditional cluster supercomputers.
We are interested in kinetic effects in high energy density plasmas relevant to intense laser-plasma interactions and inertial confinement fusion schemes. In a plasma, there may be deviations away from equilibrium on small length or time scales, or if the particles involved are very energetic. For example, the energy transferred to a plasma by ultra intense lasers is enough to generate large fluxes of relativistic electrons which stream through the plasma and set up complex electromagnetic fields. The electron motion can be strongly affected by these fields, but short-range "collisions" between particles are also important. How to correctly model these effects and use them in existing models is a challenging computational problem because of the disparate time and length scales involved and the need to correctly couple physics from multiple disciplines. We have developed a number of codes that employ direct Fokker-Planck, expansion. and particle methods in multiple dimensions to study these effects in both electrons and ions. Due to the heavy computational cost of these simulations, we write code to run on new accelerator hardware and traditional cluster supercomputers.
The figure shows the fast electron phase space; electrons are streaming through a solid density target from left to right at close to the speed of light. As they do so they induce large amplitude plasma waves, and their interaction with these waves leads to the modulated structures evident in the figure.
Line Coincidence Photopumping
D. Burridge, P. W. Hatfield and S. J. Rose
Experiments have been performed over a number of years that attempt to tailor the radiation field in a laser-produced plasma and thereby influence, by direct photopumping, the excitation and ionisation. A mechanism often considered is line coincidence photopumping, in which a strong, narrow-band source of X-rays produced by line radiation from one plasma is used to pump directly a resonant transition in a physically separate plasma.
We have modelled experiments on the ORION laser at AWE that have shown line-coincidence photopumping of H-like Cl by H- and He-like K ions in the same plasma for the first time. The experiments have shown a population enhancement in upper levels of H-like Cl which was diagnosed by enhancement of spectral line intensity of the n=4-3 transition in the H-like Cl ions. The experiments are relevant to astrophysical plasmas in which we have recently shown that a similar process operates. The experimental analysis employed both real (KCl) and null (NaCl) shots. The technique of bootstrapping was employed that allowed several different real and null experimental shots to be combined in a statistically meaningful way and resulted in a probability distribution for the enhancement.
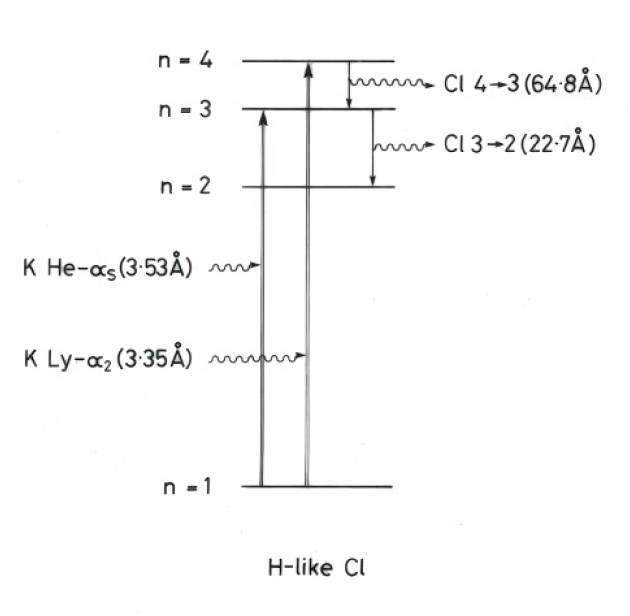
Figure shows the KCl line-coincidence pumping scheme. Enhancement was seen on the 64.8Å line.
Inertial confinement fusion (ICF)
S. J. Rose and P Hatfield
Several members of the plasma physics group at Imperial College work on Inertial Confinement Fusion (ICF), and we have strong links with Lawrence Livermore’s National Ignition Facility (NIF) in California, where the world's largest inertial confinement fusion experiment is based.
Many researchers in the plasma physics group have an interest in Inertial Confinement Fusion (ICF), especially through the Centre for Inertial Fusion Sciences (CIFS). The recent breakthrough at the US National Ignition Facility (NIF) has completely altered the fusion landscape and we are particularly working on using the output from a burning ICF plasma to probe aspects of fundamental science from particle physics to cosmology.
Probing Iron Opacity - Simulations of a Marshak Wave Through Iron Oxide Foam
K. McLean and S. J. Rose
Experimental evidence in recent years has shown that our understanding of radiative opacity in high energy density environments is not complete. Measurements of iron opacity, under conditions similar to those expected in the solar tachocline, were performed in Sandia National Laboratory. Results suggested that there exists additional contributions to radiative opacity which are, to this date, not completely accounted for in theory. In an attempt to validate the results from this experiment, iron opacity is set to be measured in an independent manner; by sending a radiation wave, known as a Marshak wave, through low density Iron Oxide foam.
The experiment will be performed on the National Ignition Facility due to it's capability of providing a sufficiently high hohlraum drive energy to ensure the Marshak wave remains supersonic for the entirety of the experiment. To do this, intense lasers interact with the gold interior of the hohlraum, creating an X-ray bath which is used to drive the Marshak wave from one end of the foam.
To analyse the experimental sensitivities to radiative opacity and specific heat capacity (how much energy is required to increase the material temperature), we have carried out simulations which are resolved spatially (1D), temporally and in photon frequency space. Analysis of these simulations provides us with estimates of the time it takes for the Marshak wave to reach the end of the foam and 'breakout'. Subsequently, the temporally resolved flux exiting the foam can be obtained for multiple different input opacity spectra and provide insight into the underlying radiative opacity of iron, which can then be compared to the result discussed above. Generally, the theory of Marshak waves predicts that a higher opacity will cause the wave to propagate through the foam at a slower rate.
Video shows a spectrally resolved simulation of a Marshak wave propagating through an iron-oxide foam. The dashed line tracks the Planckian drive from the hohlraum which drives the wave. The colormap tracks the radiation energy density.
energy_resolved_front_3D_with_planckian
Free Electron Relativistic Correction Factors to Excitation and Ionisation Rates in a Plasma
J. Beesley and S. J. Rose
When calculating rates of collisional excitation and ionisation the free electrons in a plasma are usually taken to follow the Maxwell-Boltzmann distribution. This means that they are treated classically, which is valid when both quantum mechanical and relativistic effects are insignificant. We have worked on accounting for relativistic effects.
If we use an empirical energy-dependent expression for the cross section, then special relativity affects our expression for total collisional excitation and ionisation rates for two reasons. First, electrons at a given energy travel at a lower velocity. Second, the electrons’ energy state occupation is changed from the Maxwell-Boltzmann to Maxwell–Jüttner.
We calculated the ratio of collisional rates calculated using special relativity to those calculated using classical mechanics. The rates were calculated from simple empirical formulas for the cross sections. The simple empirical cross sections depend on a single parameter: the threshold energy of the reaction. The ratios serve two purposes. First, they act as estimates for regimes in which accounting for special relativity is important. Second, they can be used as approximate correction factors to be applied post hoc to collisional rates calculated using classical mechanics from more sophisticated cross sections. We have found that the relativistic correction is significant in regimes potentially important to galactic intracluster media and diagnostic dopants in burning ICF plasmas.
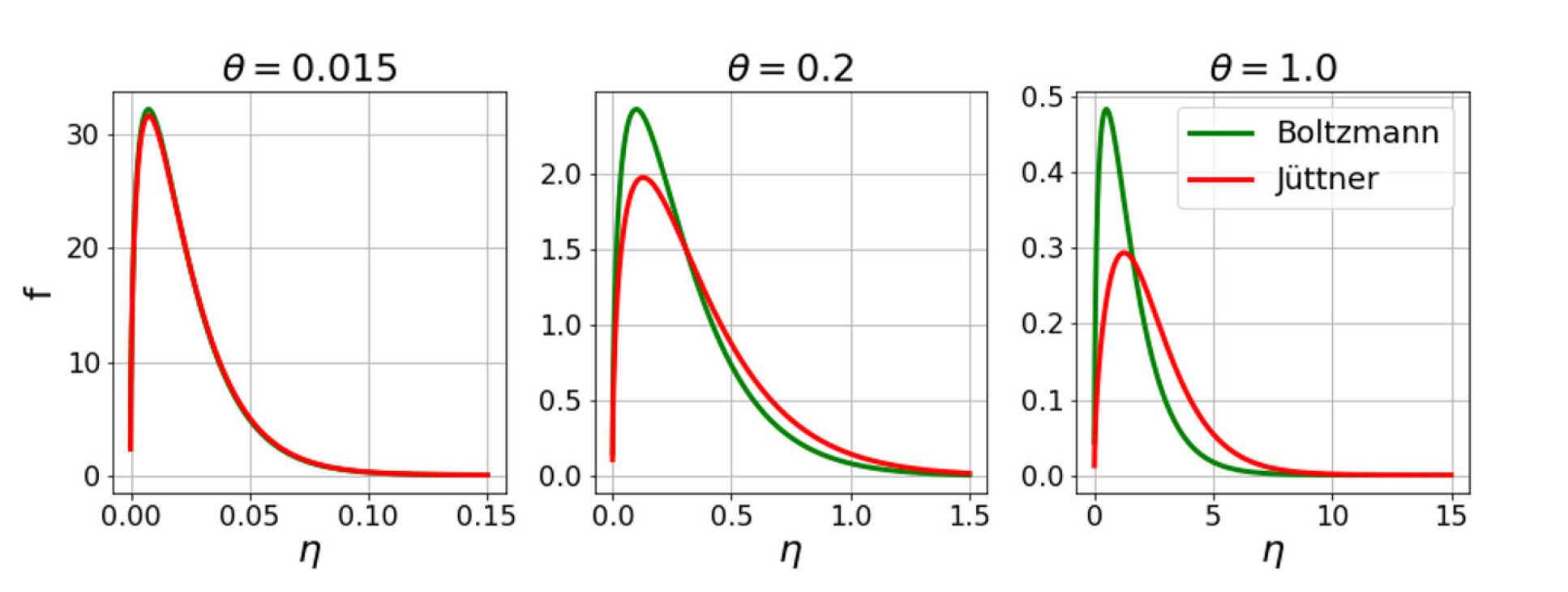
Figure shows Maxwell–Boltzmann and Maxwell–Jüttner distributions plotted against reduced kinetic energy (η = ε/kT - where ε is the electron kinetic energy), for a range of temperatures θ = kT/mc2.