About

Ben now holds a faculty position in the School of Mathematics at the University of Edinburgh (UE), with his UE web page available here. The information below was of relevance whilst a postdoctoral research associate in the Complex Multiscale Systems group.

I was a postdoctoral research associate in the  lead by Professor Serafim Kalliadasis in the Department of Chemical Engineering at Imperial College London.  Prior to this, I was a postdoctoral researcher with Professor Volker Betz (now at TU Darmstadt) in the Mathematics Institute at the University of Warwick, where I had previously completed my PhD under the supervision of Professor Gero Friesecke (now at TU Munich).

My current research is described below. In general I am interested in the derivation and analysis of reduced models for complex physical systems. In particular, I use a synergistic approach combining modelling, mathematical analysis and numerics to study phenomena in a wide range of mathematical physics including the electronic structure of atoms and molecules, quantum molecular dynamics, soft matter physics and complex fluids.

If you wish to contact me, you can email me at b.goddard@imperial.ac.uk.

Current Research

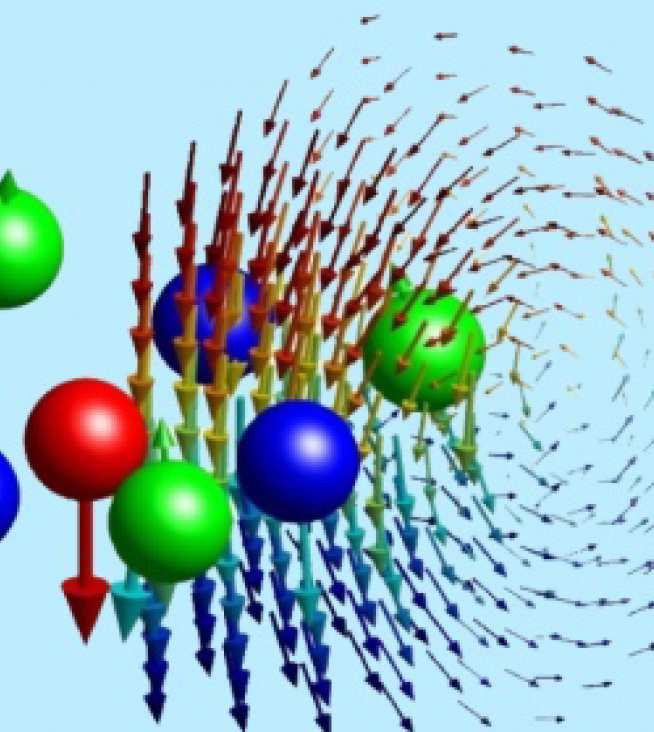
My research focusses on understanding multiscale phenomena in classical fluids.  This requires a careful combination of modelling, rigorous mathematical analysis and numerics.  Since the experimental observation of Brownian motion in the 19th century and the foundation of statistical mechanics by Einstein at the start of the 20th century, colloidal fluids (consisting of many microscopic particles suspended in a fluid bath) have been model systems for both experimental and theoretical scrutiny.  Typical examples of colloidal fluids are milk, blood and ink, and recent advances in biophysics and nanotechnology have stimulated great interest in the dynamics of such soft matter.

Due to the large numbers of particles, direct computation of the dynamics becomes intractable and reduced models are necessary. Ideally, we would like reduced equations with dimension independent of the number of particles. In recent years one such class of models, known as dynamical density functional theories (DDFTs), has received increasing attention. Existing DDFTs neglect either the inertia of the colloidal particles, or hydrodynamic interactions (bath-mediated forces), or both. However, these effects are crucial for understanding the dynamics of many colloidal systems and a more general DDFT is required.

We have rigorously derived a DDFT formalism including all crucial physical effects, which contains many existing DDFTs as special cases.  Via a rigorous homogenization argument, we have shown that the true DDFT in the high friction limit differs from that obtained by more heuristic arguments.  In particular, the rigorously-derived DDFT included a density-dependent diffusion tensor. We have also implemented an efficient numerical scheme based on the extension of spectral methods to integro-partial-differential equations to solve DDFTs. The scheme allows us to demonstrate the excellent agreement with the full underlying stochastic dynamics for a range of systems and to takle a wide range of problems in soft matter.