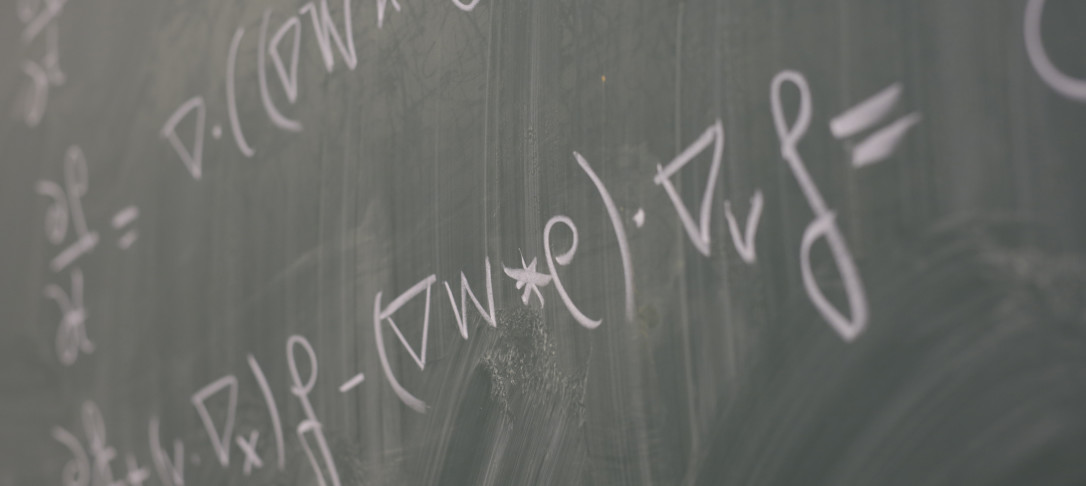
Title
Homogenisation theory as a motivation for stochastic fluid mechanics
Abstract
Geophysical fluid dynamics (GFD) often exhibit rich dynamical complexity and steep computational costs. Stochastic parametrisations are a current and fruitful research area in rendering simulations more tractable for forecasting.
In this talk we discuss a mathematical procedure for approximating multi-time deterministic chaotic systems with randomly selected initial conditions by stochastic differential equations. This is known as stochastic homogenisation. We apply homogenisation to obtain one such stochastic parametrisation for fluids, stochastic advection by Lie transport (SALT) and derive structure preserving stochastic equations via a variational principle. A homogenisation approach to stochastic fluid dynamics is particularly well suited given multiple time scales and sensitivity to initial conditions that are naturally occurring in GFD.
We shall discuss the insight obtained from this approach, links to stochastic analysis, as well the surprising phenomena of noise induced drift terms that often lead to dramatic changes in dynamical behaviour.
Please note that the seminar will take place in person in room 642 of Huxley Building.


