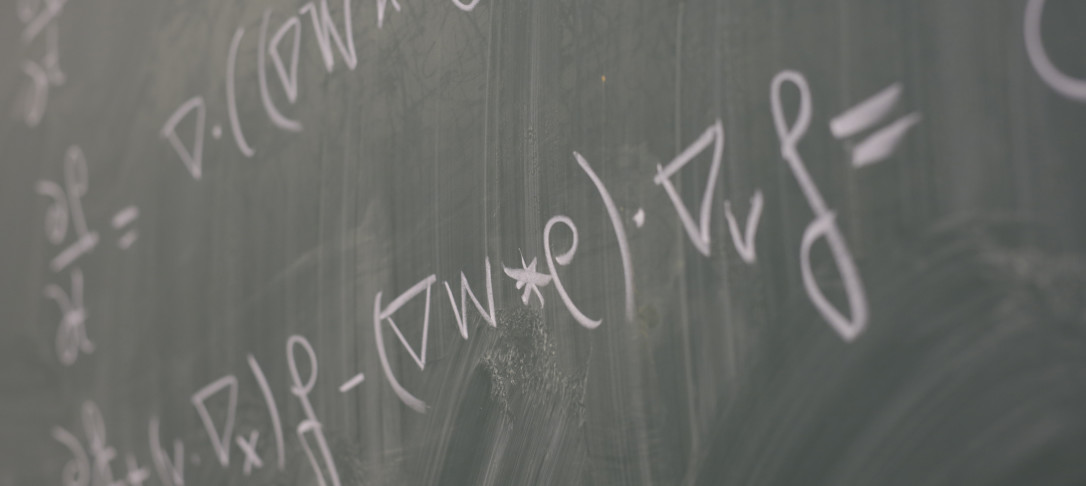
Title
On asymptotic stability and Strichartz estimate for self-similar blowup of mass supercritical NLS
Abstract
For slightly mass supercritical nonlinear Schrodinger equations (NLS), self-similar blowup has been proven to exist and generate stable blowup dynamics. However, the asymptotic stability was missing. With suitable self-similar profiles constructed recently, we take one further step to show their finite codimensional asymptotic stability. One core ingredient is a Strichartz estimate for the linearized matrix operator, where an “enhanced dispersion” phenomenon for the propagator is exploited.
Please note that the seminar will take place in person in room 642 of Huxley Building.


