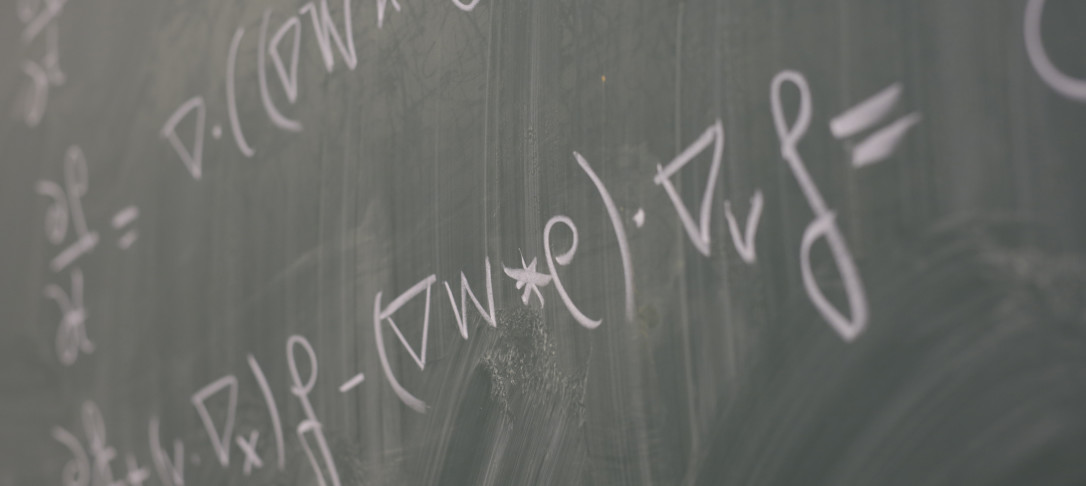
Title
Vortex dynamics for the Gross-Pitaevskii equation
Abstract
The Gross-Pitaevskii equation in the plane arises as a physical model for an idealized, two-dimensional superfluid. We construct solutions to this equation with isolated vortices of degree +1 and -1, corresponding to concentration points of the associated fluid vorticity. The leading order vortex dynamics is governed by the classical Kirchhoff law, and our method provides detailed information on the asymptotic profile of the solutions near the vortex set. A key feature of the construction are new estimates related to the stability of multiple-vortex configurations. This is joint work with Manuel del Pino and Monica Musso.
Please note that the seminar will take place in person in room 642 of Huxley Building.


