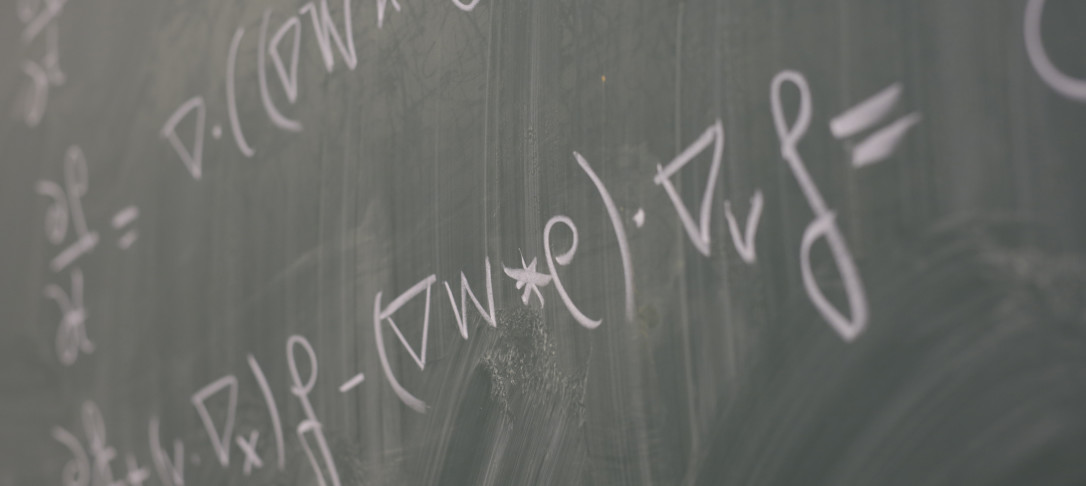
Title
Sharp non explicit blow-up profile for a nonlinear heat equation with a gradient term
Abstract
We consider the semilinear heat equation with a pure power nonlinearity, which is a less complicated version of some famous PDEs,
where we can observe the phenomenon of blow-up that occurs in some solutions for these equations. We will recall some famous results
related to a class of these solutions, called solutions of type I, such as the existence and the notion of blow-up profile near the
singularity.
Following that, we will consider a nonlinear heat equation with a nonlinear term depending on the unknown and its gradient, which is a
more general case than the previous equation. In the earlier literature, we have the existence of a stable blow-up solution with an explicit profile. By pursuing a limited development, we are trapped in scales of order $\frac{1}{\log |T − t|^\nu}$ where $T$ is the blow-up time. In this work, we are able to provide a sharper description up to $|T −t|^\mu$. The price to pay is to replace the explicit profile by a non explicit profile, which is in a fact a well-prepared blow-up solution of the semilinear heat equation with a pure power nonlinearity.
Please note that the seminar will take place in person in room 144 of Huxley Building.


