By Musab Khawaja
Spinodal decomposition is the process through which a solution of at least two components separates spontaneously and uniformly into distinct regions or phases. The kinetics of this process for a binary solution can be modelled using the Cahn-Hilliard equation,
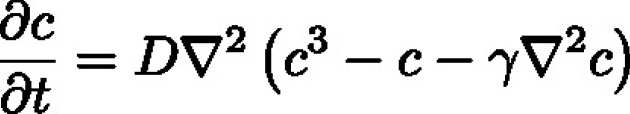where c is a measure of concentration, D is the transport coefficient and gamma is a constant that will determine the length scale over which the decomposition occurs.
This figure shows the evolution in time of an initially random mixture of two components. We can see the components gradually accumulating in separate regions. There are two length scales that play a part. Large fluctuations are smoothed out by diffusion. Meanwhile small local fluctuations want to create lots of interfaces between different regions, which is energetically expensive. This results in an optimal size of fluctuation that spreads the quickest i.e. a characteristic transition length. This is determined by the parameter gamma.
The above demonstration shows the evolution of some initial random state for 200 time units
The above demonstration takes the same initial state, but looks at the effect of gamma on the final state after the same amount of time as before. We can see that gamma does have an effect on the width of the regions between phases (in yellow). Theory predicts these regions should scale as √gamma, which is what we observe.
The above final demonstration puts you in control. Play with the different parameters and see what happens. The size of the domain is n x n cells and dt is the time step used for numerical integration. These regions are also periodic - you can see that they wrap round from one side of the square to another. To visualise this, there is also the option of mapping the results onto a cylinder or sphere.