By Vincent Huair-Yu Chen
My simulation demonstrates the Ising model, a simple theoretical de- scription of ferromagnetism in statistical mechanics. The system is a simple n-by-n lattice of spins which are either spin up (black) or spin down (white) with periodic boundary conditions applied in both dimensions. Spin-to-spin interactions are allowed only between direct neighbours. A variable uniform external magnetic field can also be applied.
The total energy of this system, E, in a given configuration is given by:
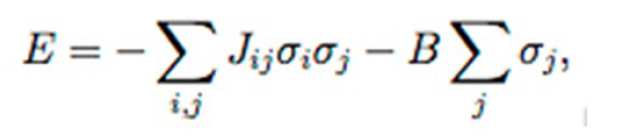
where sigma i is the spin (+1 for spin up and -1 for spin down) atsiteiandBisthe magnitude of the magnetic field. Jij represents the interaction between sites i and j and is a constant (J) if i and j are direct neighbours or 0 otherwise. In my simulation, the equation is normalised such that J = 1, therefore the quantity B in my demonstration can be viewed as the ratio of the magnetic field relative to the site-to-site interaction.
The Metropolis algorithm is utilised to control the evolution of the system. In each step, a random spin is picked and proposed to have its spin flipped. The probability, p, that its spin is actually flipped is governed by the change in energy between its current and proposed configurations (delta E):
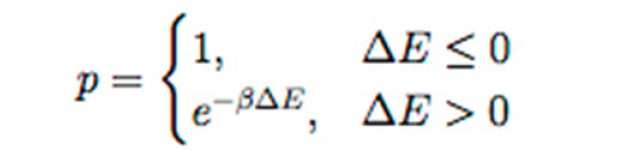
beta = 1/(k*T) and can be varied in the demonstration. A live graphic of the configuration of spins is displayed along with a plot of the system energy over time.