Control of Wave Energy Converters
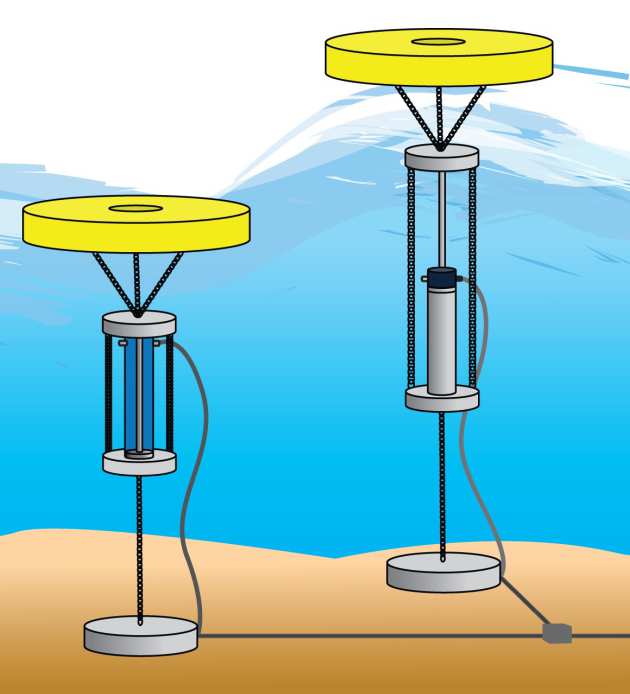
This project studies the control problems arise from wave energy converter (WEC) application, along with the related numerical optimization and discretization problems.
In this project, two types of control problems are studied, the first one is known to wave energy community as passive control. In particular, the latching, declutching and latching-declutching controls. We proposed an unified model based on hybrid system (a mix of discrete event system and continuous time system) for these passive control implementations. With our model, we propose a formulation that turns the optimal control problem into a small dimensional discrete optimization problem, where the only decision variables are the bounds on the latching time and power-take-off time.
To solve the discrete optimization problem, we studied the derivative-free optimization algorithms and revealed a suffcient convergence condition for general directional direct-search algorithms. Based on the specific problem we have, we proposed a coordinate-search algorithm, which is one of the directional direct-search algorithm. The algorithm is able to effciently solve small dimensional problems with discrete decision variables.
The state constraints were scarcely discussed in the wave energy control literatures. For declutching control, we proposed a formulation which is able to incorporate state constraints. The formulation gives a mixed-integer nonlinear optimal control problem, which is very hard to solve. Based on a technique known as variable time transform, we are able to reformulate the mixed-integer nonlinear optimal control problem into a large-scale nonlinear programming (NLP) problem. The transformed NLP problem can be solved effciently by NLP solvers such as interior point method used in IPOPT.
The second type of control problem we have investigated in this project is the active force control. Under the assumption that the generator can also be a motor, an active force can be asserted to the wave energy converter and thus form a linear controlled system. We proposed a simple optimal control problem formulation that in theory there is no convexity guarantee. However, we demonstrated that the discretized large-scale NLP problem can be convex and the convexity related only to the system parameters and is independent from the excitation force and current state. This important feature implies that we are always able to choose a set of system parameters off-line so that for the online closed-loop implementation, all the optimization problems are convex. In practice, for a large range of parameter sets, the resulted optimization problems are convex.
CAP People
- Zhe Feng
- Dr. E.C.Kerrigan


